【解答・解説】早稲田理工物理2025 第2問 -電磁気-
2025年度の早稲田大学基幹・創造・先進理工学部物理第2問を解説します。電磁気の単元です。
この記事に関連するQ&A
問題
問題
以下の問題文および図は,2025年度早稲田大学基幹・創造・先進理工学部入試問題物理第2問から引用しています(一部見やすさ等のためライターが修正・変更した部分があります)。
以下の問に答えよ。
電磁場中での荷電粒子の問題を考える。ただし,真空中の運動を扱い,重力の影響は考えないものとする。 まず,図1 のような領域 I 〜 III の3つの部分から構成される装置内での荷電粒子の運動を考える。
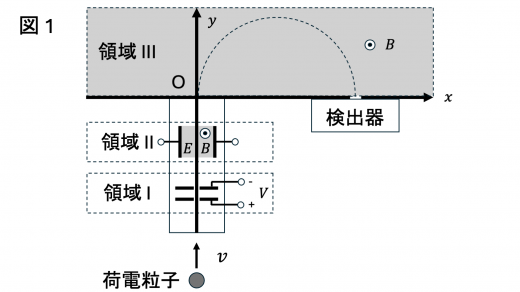
各領域内の電磁場は他の領域には影響を与えず,極板間の電磁場は一様であるとする。原点 O と 軸, 軸の向きを 図1 のように設定し,紙面垂直に裏から表の向きを 軸正の向きとする。
領域 I では,平行平板電極が 図1 のように置かれている。ここに,正の電荷 をもつ質量 の荷電粒子が平行平板電極に対して垂直 ( 軸上) に初速 で入射した。2つの電極板には 荷電粒子が通り抜けられる小孔が開いており,電極板間には 図1 のように電圧 がかけられている。小孔は 軸上にあり,小孔による電磁場の影響は無視できるものとする。
問1 荷電粒子がこの電極板間を通過するあいだに得るエネルギーはいくらか。
問2 荷電粒子がこの電極板間を通り抜けた直後の荷電粒子の速さはいくらか。
続いて,荷電粒子は領域 I から領域 II に進入した。領域 II では 図1 のように平行平板電極が置かれ,2枚の電極板間には強さ の電場が生じている。また,電極板間内では 軸正の向きに磁束密度の大きさ の一様な磁場がかけられている。 荷電粒子はこの電極板間を 軸正の向きに直進した。
問3 荷電粒子がこの電極板間で電場から受ける力の大きさを の関数として答えよ。また,電場から受ける力の向きを,座標軸とその正負で答えよ。
問4 荷電粒子がこの電極板間で電場から受ける力の大きさを の関数として答えよ。また,磁場から受ける力の向きを,座標軸とその正負で答えよ。
問5 領域 II における荷電粒子の速さを と を用いて答えよ。
問6 初速 を を用いて答えよ。
続いて,荷電粒子は 問5 の速さで領域 II から領域 III に進入した。領域 III でも 軸正の向きに磁束密度の大きさ の一様な磁場がかけられている。このとき,荷電粒子は半径 の半円軌道で運動し,検出器で観測された。
問7 荷電粒子が領域 III に進入してから検出器に到達するまでの時間を を用いて答えよ。
問8 比電荷 を を用いて答えよ。
この装置の原理を用いることで,入射した荷電粒子の質量を分析することができる。ここでは,荷電粒子の入射位置や検出器の位置は変えないものとし,電場や磁場を制御することで質量分析を行う。
問9 正の電荷 をもつ質量 の荷電粒子が 問5 の速さで 軸に沿って領域 III に進入した場合を考える。この荷電粒子は 問7 と同じ軌道で運動した。このときの領域 III の磁束密度の大きさは の何倍か。
次に,図2 のように 図1 と同様の座標軸を設定し, 軸正の領域に一様な磁場がかけられている場合を考える。
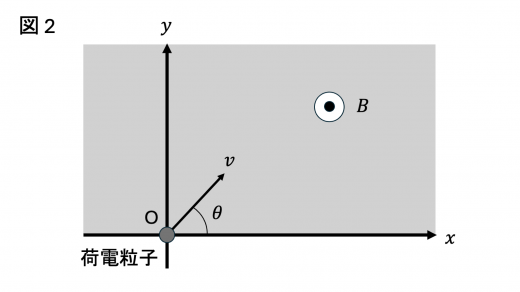
この磁場は磁束密度の大きさが で, 軸正の向きであった。いま,正の電荷 をもつ質量 の荷電粒子を,原点 O から 平面内に初速 ,角度 で入射したところ,荷電粒子は磁場中を運動し 軸上に戻ってきた。
問10 荷電粒子が 軸上に戻ってきたときの 座標,荷電粒子が運動しているときの 座標の最大値をそれぞれ を用いて答えよ。
最後に,図2 と同じ磁場中に,原点 O から荷電粒子 A (電荷 ,質量 ) を入射した場合と荷電粒子 a (電荷 ,質量 ) を入射した場合をそれぞれ考える。 軸正の向き () に荷電粒子 A と荷電粒子 a を異なる初速で入射したところ,2つの荷電粒子は同じ軌道を用いて運動した。この入射条件のもとで2つの荷電粒子を区別するため,さらに 図3 のように 図2 と同様の座標軸と磁場を設定し, 軸正の方向に大きさ の一様な電場をかけた。
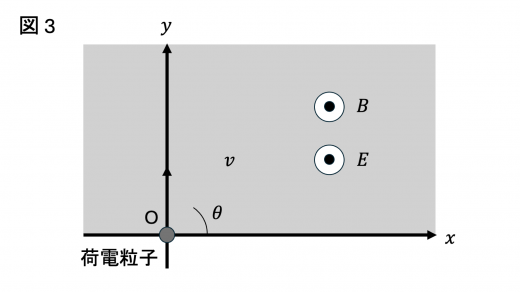
問11 荷電粒子 a が入射してから 平面に到達するまでの時間は,荷電粒子 A が入射してから 平面に到達するまでの時間の何倍か。
問12 平面において荷電粒子 A が到達する位置の 座標を を用いて答えよ。
電磁場中での荷電粒子の運動に関して考察する問題です。 高校物理の分野では頻出の問題設定です。
解答例
解答例
(1)
荷電粒子は領域 I の運動により,位置エネルギーの大きいところから小さいところへと到達するので,その位置エネルギーの差分をエネルギーとして得たと考えることができます。
したがって,求めるエネルギーは
となります。
(2)
電極板間を通り抜けた直後の荷電粒子の速さを とします。 力学的エネルギー保存則 (力学的エネルギー保存則の導出と例題) により
と求められます。
(4)
ローレンツ力の大きさと向きが簡単に求められるので,そちらから先に求めます。
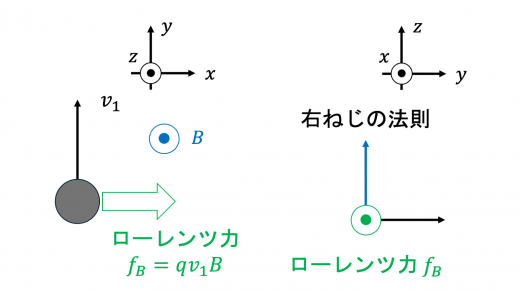
ローレンツ力の大きさの公式 (ローレンツ力の意味と式|磁場中の荷電粒子の運動) より,ローレンツ力の大きさ は
このローレンツ力の大きさの向きは,右ねじの法則 (電流と磁束密度の関係) より, 軸正の向きとなります。
(3)
荷電粒子が電場から受ける力の大きさ (電場・磁場・電荷密度・電流密度|電磁気学における基本的な物理量) は
領域 II 内で荷電粒子が 軸正の向きに直進したことから,この領域内で荷電粒子にはたらく力はつり合っていることがわかります。 (4)の答えより,荷電粒子が電場から受ける力の向きは 軸負の向きとなります。
(5)
この力のつりあいから を別の表式で求めることができます。すなわち より
と表すことができます。
(6)
(2)および(5)の結果より,初速 を
と表すことができます。
(7)
領域 III ではローレンツ力のみがはたらくので,この領域で荷電粒子は等速円運動をすることがわかります。 この等速円運動の角振動数を とすると,円運動の運動方程式 (円運動とは|円運動における加速度・向心力・遠心力) より
荷電粒子が検出器に到達するまでの時間 は,この等速円運動の 1/2 周期と等しく,したがって
と表すことができます。
(8)
一方,円運動の速さの公式より
(7)での議論と合わせて,比電荷 は
と表すことができます。
(9)
電荷 ,質量 の荷電粒子が で 軸に沿って,磁束密度 が加わっている領域 III に進入したとき,その等速円運動の軌道が であったとします。(8)の結果よりこの結果は
これらより を2通りの方法で表すことができ
ゆえに,磁束密度の大きさは の 倍となっています。
(10)
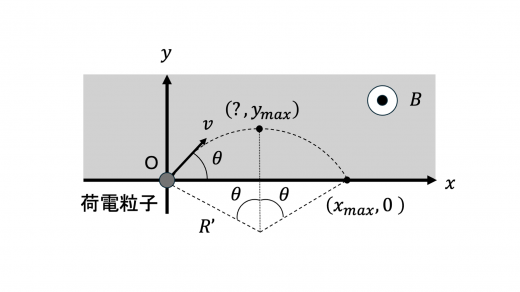
荷電粒子が等速円運動を行うことにより,このときの の軌道は上図のようになると考えられます。
この円運動の半径を とおくと,等速円運動の運動方程式より
したがって,荷電粒子が 軸に戻ってきたときの 座標 は
また,運動しているときの 座標の最大値 は
と,それぞれ求めることができます。
(11)
(11)・(12) では,「荷電粒子 A / a が 平面に到達する」を,「荷電粒子 A / a が原点から運動を初めて最初に 平面に到達する」と解釈した答えを載せます。
荷電粒子 A,a の初速をそれぞれ とおきます。 2つの荷電粒子の円運動の軌道が等しくなることから,(10)での議論より,円運動の半径 について等式を立てることができ,これらの初速について
という関係があることがわかります。
一方,磁束密度に加えて 軸正の方向に電場 をかけることを考えます。 このときの荷電粒子の運動は, 平面内のローレンツ力による等速円運動と, 軸正の方向のクーロン力による等加速度運動を組み合わせた,螺旋運動を行います。
空間でこのような運動を行う荷電粒子が,出発してから初めて再び 平面に到達するまでの時間は, 平面内の等速円運動の 周期となります。
荷電粒子 A・a それぞれのこの 周期 をそれぞれ , 角振動数をそれぞれ とします。このとき
ゆえに
となるので,求める倍率は 倍となります。
(12)
荷電粒子 A の 軸方向の運動を考えます。この等加速度運動の加速度は であり, 軸方向の荷電粒子 A の初速度が なので,運動を初めてから 秒後の荷電粒子 A の 座標は
したがって,荷電粒子 A が運動を初めて最初に 平面に到達したときの 座標 は
ここで, より
ゆえに
となります。
(注)「荷電粒子 A / a が 平面に到達する」を「一般に,荷電粒子 A / a が原点から運動を初めて 回目に 平面に到達する」と考えてみます。
荷電粒子 A が原点から運動を初めて 回目に 平面に到達する時刻 は
となります。(12)の答えとして,一般に荷電粒子 A が 平面内に到達する際の 座標を全て列挙すると解釈すると,そのような座標は
となります。
電磁場での荷電粒子の運動は,大学入試では頻出です。 一度触れていたかどうかで本番での処理能力がかなり異なってきます。











