【解答・解説】東科大物理2025 第3問 -熱力学-
2025年度の東科大物理第3問を解説します。熱力学の単元です。
この記事に関連するQ&A
問題
問題
以下の問題文および図は,2025年度東京科学大学入試問題物理第2問から引用しています(一部見やすさ等のためライターが修正・変更した部分があります)。
十分な長さを持つシリンダー内に質量が無視できるピストンがあり,それらにより閉じ込められた気体の状態変化について考える。大気圧を ,気体定数を ,重力加速度の大きさを とし,以下の設問に答えよ。
[A] 図1のように,断面積 のシリンダーが水平な床の上に鉛直に固定されている。
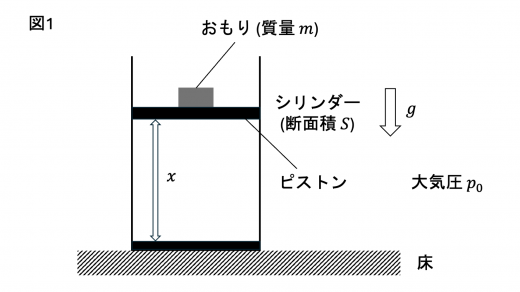
ピストンはシリンダー内の気体と大気を仕切ることができ,傾くことなく鉛直方向に滑らかに動く。シリンダー底面からピストンの下面までの距離を用いて,ピストンの位置を と表す。シリンダー,ピストンは断熱材でできている。
最初,質量 のおもりを乗せたピストンが で静止しており,ピストンの下側に温度 の単原子分子理想気体が閉じ込められていた。
(a) シリンダー内の気体の圧力を求めよ。
次に,ピストンに外力を加え,ピストンの位置を までゆっくりと移動させ,シリンダー内の気体を圧縮した。
(b) ピストンの位置 におけるシリンダー内の気体の温度を求めよ。
© この圧縮過程で,シリンダー内の気体がされた仕事を求めよ。
[B] 図2のように,同じ断面積 を持つシリンダー A,シリンダー B が水平な床の上に鉛直に固定されており,コックと細孔栓のついた細い管でつながっている。
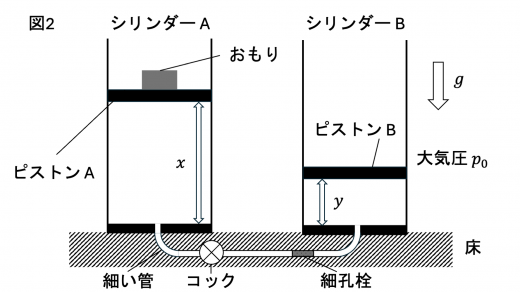
ピストン A,ピストン B は,それぞれシリンダー A 内,シリンダー B 内の気体と大気を仕切ることができ,傾くことなく鉛直方向に滑らかに動く。ピストン A にはおもりが乗っており,ピストン B にはおもりが乗っていない。細孔栓は細孔のあるつめものであり,細孔栓を用いることでシリンダー A 内,シリンダー B 内の気体の圧力をそれぞれ一定に保ちながら,気体を移動させることができる。シリンダー,ピストン,コックと細孔栓のついた細い管は断熱材でできている。シリンダー底面からピストンの下面までの距離を用いて,ピストン A の位置を ,ピストン B の位置を と表す。
最初,コックは閉じられており,ピストン A は に,ピストン B はシリンダーの底 () に静止している。ピストン A の下側には温度 の単原子分子理想気体が閉じ込められており,気体の圧力は である。
次に,コックを開き,ピストン A にかかる力のつり合いを保ちながら,ピストン A をゆっくりと下方に動かした。コックを開いた直後の気体の状態を状態1とよぶ。ピストン A を下方に動かしていく過程において,シリンダー A 内の気体の一部が,細孔栓のついた細い管を通ってシリンダー B に流入し,ピストン B はゆっくりと上方に移動した。このとき,シリンダー A 内の気体の温度は のままであり,ピストン B にかかる力は常につり合っていた。
ピストン A が から まで移動したとき,ピストン B は から に移動したとする。このとき,シリンダー B 内の気体の温度を ,気体全体の内部エネルギーを とそれぞれ表す。
(d) ピストン B の位置 を, のうち必要なものを用いて求めよ。
(e) シリンダー A 内の気体がされた仕事 ,シリンダー B 内の気体がした仕事 を, のうち必要なものを用いて求めよ。
(f) シリンダー A,シリンダー B に閉じ込められた気体全体に対して,熱力学第1法則を考える。ピストン A が から まで移動したときの内部エネルギーの変化は, を用いて以下のように書ける。
このことから,シリンダー B 内の気体の温度は
と求まる。空欄 に当てはまる数式を求めよ。
さらに,ピストン A をシリンダー A の底 () まで動かしたとき,気体はシリンダー B のみに閉じ込められた。この気体を状態 2 と呼ぶ。
(g) 状態1から状態2への過程における仕事 は,それぞれ状態1もしくは状態2における気体の温度,圧力,体積により表せる。このことを用いると,温度 ,圧力 ,体積 の気体に関して,内部エネルギー と の和で表される量
が,この過程の前後で変化していないことがわかる。 のうち必要なものを用いて空欄 を表せ。
また,式 (3) は単原子分子理想気体の場合,気体の物質量 を用いて
と書ける。 のうち必要なものを用いて空欄 を表せ。
[C] 設問 [B] での設定において,理想気体ではなく,実在の気体 (実在気体) を用いて同様の操作を行う。実在気体は,理想気体とは異なり,分子間にはたらく力と分子自身の体積を無視できない。そのため,式 (4) に補正が加わり,
が過程の前後で一定に保たれる。ここで は気体によって決まる正の数であり, は実在気体の物質量である。
最初,コックは閉じられており,ピストン A は に,ピストン B はシリンダーの底 () に静止している。ピストン A の下側には温度 の実在気体が閉じ込められており,その気体の圧力は である。
次に,コックを開き,ピストン A にかかる力のつり合いを保ちながら,ピストン A をゆっくりと下方に動かした。コックを開いた直後の気体の状態 (状態1) から,シリンダー B のみに閉じ込められた気体の状態 (状態2) への過程において,シリンダー A 内の気体の温度は のままであり,ピストン B にかかる力は常につり合っていた。
(h) 過程の前後で が一定に保たれることを利用することで,状態2におけるシリンダー B 内の実在気体の温度 は
と表される。ここで, は理想気体を用いた場合の状態2 () における気体の温度である。状態1,状態2における気体の体積をそれぞれ とし, のうち必要なものを用いて空欄 を表せ。
理想気体・実在気体に関する問題です。問題文をよく読み,変化の過程で保たれている物理量が何かを正確に把握することが大切です。
解答例
解答例
[A]
(a)
求めるシリンダー内の圧力を とします。シリンダーについて,力のつり合い (力のつりあい・作用反作用との違い) より
と求められます。
また,このときの理想気体について,物質量を とすると,状態方程式より
が成り立っていることに注意します。
(b)
シリンダー内の単原子理想気体の圧縮は,断熱変化 (断熱変化におけるポアソンの式の導出) になっています。したがって,ポアソンの公式より, (一定) が成り立ちます。理想気体の状態方程式 (ボイル・シャルルの法則と状態方程式) と合わせると (一定) が成り立ちます。
これより, での気体の温度を とすると
と求められます。
©
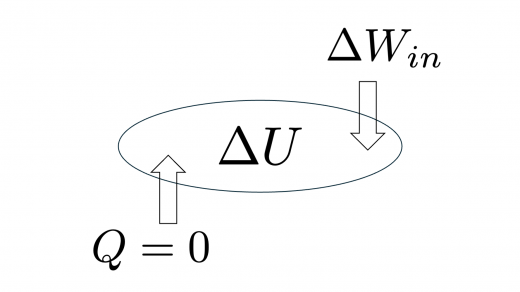
シリンダー内の気体がされた仕事を とします。この変化が断熱変化である () ことに注意して,熱力学第一法則 (熱力学第一法則|仕事と内部エネルギーの関係)より
と求められます。ここに,単原子理想気体の内部エネルギー は と表されることを用いました (気体の内部エネルギーの意味と公式,求め方)。
[B]
(d)
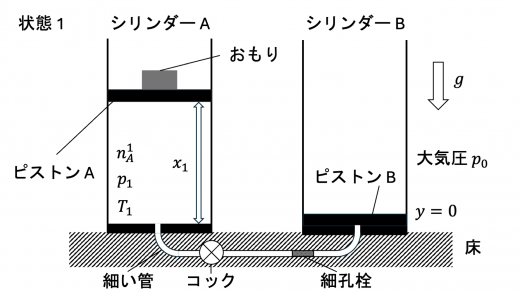
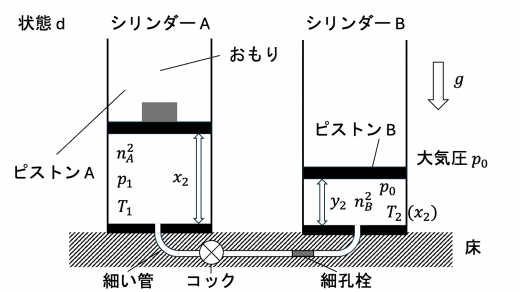
上図で表される状態を状態1,状態 d とします。状態1のシリンダー A,状態 d のシリンダー A・B 内の気体の物質量をそれぞれ とすると,理想気体の状態方程式より
また,この変化で気体の総量は保存されているので
(d-1)・(d-2)・(d-3) 式を (d-4) 式に代入して
のように求められます。
(e)
問題文より,状態1から状態 d への変化中,ピストン A・B それぞれに加わる力は常につり合っていることがわかります。
したがって,シリンダー内の気体がされた仕事 は
また,シリンダー内の気体がした仕事 は
と表すことができます。A については「された仕事」,B については「した仕事」を求めることに注意してください。
(f)
シリンダー A・B に閉じ込められた気体全体に対して熱力学第一法則を考えます。
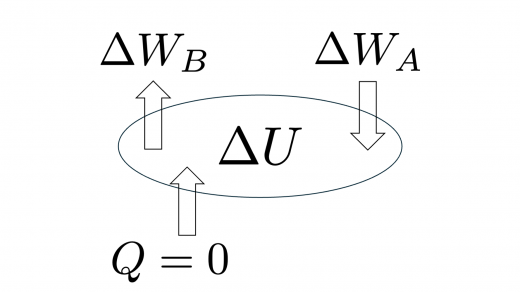
は「気体がされた仕事」, は「気体がした仕事」であることに注意すると,上図のように
と表されます ((ア):)。
を内部エネルギーの公式を用いて表します。
これらを熱力学第一法則の式に代入して
について整理して
(d) の結果と比較して,シリンダー B 内の気体の温度は
と求められます ((イ):)。
(g)
ピストン A の位置が となっている状態2への過程を考えます。
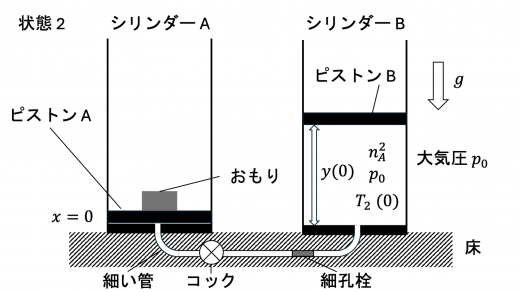
このときのピストン B の位置を とします。状態1から状態2への変化で,各ピストンに加わる力は一定なので, はそれぞれ
一方, のときの気体全体の内部エネルギー は,両状態とも気体がシリンダーのどちらか一方に存在していることより
したがって,(f) で求めた熱力学第一法則の式より
は状態1での気体の体積, は状態2での気体の体積であることより,この過程の前後で
が変化していないことがわかります ((ウ):)。
単原子理想気体のとき, は気体の物質量 を用いて表すことができます。まず,単原子理想気体の内部エネルギーの公式より
次に,理想気体の状態方程式より
したがって
となります ((エ):)。
[C]
(h)
気体が実在気体の場合は,状態1から状態2への過程の前後で
が一定に保たれることを利用します。気体の物質量を改めて とおき,状態1・2でのこの量をそれぞれ とすると
と表すことができます。
(f)(イ) の結果より であることに注意しながら式変形していきます。 より
が係数 1 で出てくるように意識しながら式変形します。
したがって,(オ): となります。
最後の設問 (h) の式変形は,問題文が提示したかたちに合うように変形する必要があり,やや難しいかもしれません。











