[A]
(a)
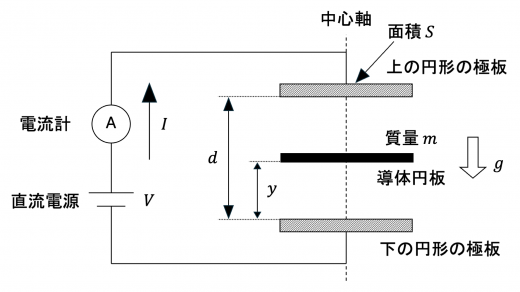
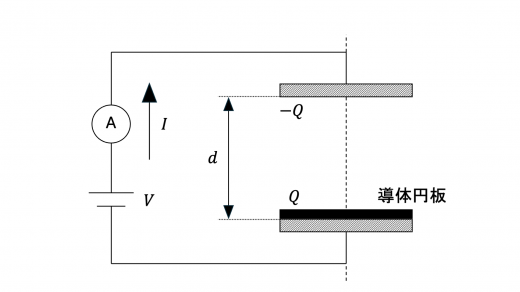
導体円板が下の極板と接触しているとき,上の極板および下の極板・導体円板によるコンデンサーの静電容量を C C C コンデンサーの理論 ) より
C = ε 0 S d
C = \varepsilon_0 \dfrac{S}{d}
C = ε 0 d S
となります。
導体円板の上面に生じる電荷を Q Q Q − Q -Q − Q
キルヒホッフ第2法則 (キルヒホッフの法則の解説と例題 ) より,導体円板の上面に生じる電荷は
V + Q C = 0
V + \dfrac{Q}{C} = 0
V + C Q = 0
∴ Q = − C V = − ε 0 S d V
\begin{aligned}
\therefore Q &= - CV \\
&= - \varepsilon_0 \dfrac{S}{d} V
\end{aligned}
∴ Q = − C V = − ε 0 d S V
と求められます。
(b) コンデンサーの公式より,上の極板と導体円板で構成されるコンデンサーが蓄える静電エネルギー U U U
U = 1 2 ∣ Q ∣ V = 1 2 ε 0 S d V 2
\begin{aligned}
U &= \dfrac{1}{2} |Q| V \\
&= \dfrac{1}{2} \varepsilon_0 \dfrac{S}{d} V^2
\end{aligned}
U = 2 1 ∣ Q ∣ V = 2 1 ε 0 d S V 2
と求められます。
[B]
©
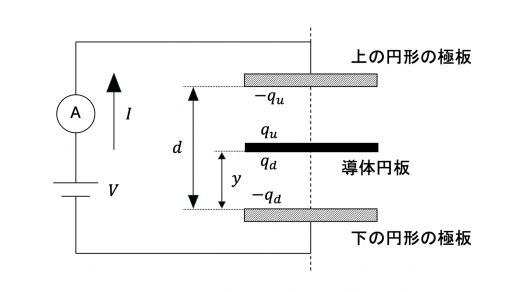
導体極板が距離 y y y q u , q d q_u, q_d q u , q d
まず,導体極板が浮上を始めてから,導体では電荷量保存則 (電荷と電気量保存の法則 ) が成り立ちます。すなわち
q u + q d = Q (1)
q_u + q_d = Q \tag{1}
q u + q d = Q ( 1 )
上の極板と導体極板の上側および導体極板の下側と下の極板からなるコンデンサーの静電容量をそれぞれ C u , C d C_u, C_d C u , C d
C u = ε 0 S d − y , C d = ε 0 S y
\begin{aligned}
C_u = \varepsilon_0 \dfrac{S}{d-y}, \quad C_d = \varepsilon_0 \dfrac{S}{y}
\end{aligned}
C u = ε 0 d − y S , C d = ε 0 y S
上図の回路においてキルヒホッフ第2法則より
V + q u C u − q d C d = 0
V + \dfrac{q_u}{C_u} - \dfrac{q_d}{C_d} = 0
V + C u q u − C d q d = 0
∴ q u ( d − y ) − q d y = − ε 0 S V (2)
\therefore q_u (d - y) - q_d y = - \varepsilon_0 S V \tag{2}
∴ q u ( d − y ) − q d y = − ε 0 S V ( 2 )
(1)・(2)式から q d q_d q d
q u ( d − y ) − ( Q − q u ) y = − ε 0 S V
q_u (d -y) - (Q - q_u) y = - \varepsilon_0 S V
q u ( d − y ) − ( Q − q u ) y = − ε 0 S V
整理して
q u = − ε 0 S d ( 1 + y d ) V (3)
q_u = - \varepsilon_0 \dfrac{S}{d} \left( 1 + \dfrac{y}{d} \right) V \tag{3}
q u = − ε 0 d S ( 1 + d y ) V ( 3 )
と求められます。
また,(1)・(3)式より
q d = Q − q u = ε 0 S d y d V (4)
\begin{aligned}
q_d &= Q - q_u \\
&= \varepsilon_0 \dfrac{S}{d} \dfrac{y}{d} V \tag{4}
\end{aligned}
q d = Q − q u = ε 0 d S d y V ( 4 )
と求められます。
(d)
上の極板と導体円板の上側および,導体円板の下側と下の極板から構成されるコンデンサーが蓄えている静電エネルギーを,それぞれ U u ( y ) , U d ( y ) U_u (y), U_d (y) U u ( y ) , U d ( y )
このとき,上下の極板と導体円板で構成される平行板コンデンサーに蓄えられた全静電エネルギー U ( y ) U(y) U ( y )
U ( y ) = U u ( y ) + U d ( y ) = 1 2 ( ∣ q u ∣ 2 C u + ∣ q d ∣ 2 C d ) = 1 2 [ 1 ε 0 d − y S { ε 0 S d ( 1 + y d ) V } 2 + 1 ε 0 y S ( ε 0 S d y d V ) 2 ] = . . . = 1 2 [ 1 + y d − ( y d ) 2 ] ε 0 S d V 2
\begin{aligned}
U(y) &= U_u (y) + U_d (y) \\
&= \dfrac{1}{2} \left( \dfrac{|q_u|^2}{C_u} + \dfrac{|q_d|^2}{C_d} \right) \\
&= \dfrac{1}{2} \left[ \dfrac{1}{\varepsilon_0} \dfrac{d-y}{S} \left \{ \varepsilon_0 \dfrac{S}{d} \left( 1 + \dfrac{y}{d} \right)V \right \}^2 + \dfrac{1}{\varepsilon_0} \dfrac{y}{S} \left( \varepsilon_0 \dfrac{S}{d} \dfrac{y}{d} V \right)^2 \right] \\
&= \quad ... \\
&= \dfrac{1}{2} \left[ 1 + \dfrac{y}{d} - \left( \dfrac{y}{d} \right)^2 \right] \varepsilon_0 \dfrac{S}{d} V^2
\end{aligned}
U ( y ) = U u ( y ) + U d ( y ) = 2 1 ( C u ∣ q u ∣ 2 + C d ∣ q d ∣ 2 ) = 2 1 [ ε 0 1 S d − y { ε 0 d S ( 1 + d y ) V } 2 + ε 0 1 S y ( ε 0 d S d y V ) 2 ] = ... = 2 1 [ 1 + d y − ( d y ) 2 ] ε 0 d S V 2
と求められます。
これは,y = 0 y = 0 y = 0
(e)
このコンデンサーの系は,コンデンサーが蓄える全静電エネルギー U ( y ) U (y) U ( y ) K ( y ) K(y) K ( y ) U g ( y ) U_g (y) U g ( y ) E ( y ) E (y) E ( y ) 0 0 0 y y y W V ( y ) W_V (y) W V ( y ) 熱力学第一法則|仕事と内部エネルギーの関係 )
E ( y ) − E ( 0 ) = W V ( y )
E(y) - E(0) = W_V (y)
E ( y ) − E ( 0 ) = W V ( y )
∴ ( U ( y ) − U ( 0 ) ) + ( K ( y ) − K ( 0 ) ) + ( U g ( y ) − U g ( 0 ) ) = W V ( y ) (5)
\therefore (U(y) - U(0)) + (K(y) - K(0)) + (U_g (y) - U_g (0)) = W_V (y) \tag{5}
∴ ( U ( y ) − U ( 0 )) + ( K ( y ) − K ( 0 )) + ( U g ( y ) − U g ( 0 )) = W V ( y ) ( 5 )
という関係が成り立ちます。
y = 0 y = 0 y = 0 A ] で考察していた状態であり,このとき導体極板が静止していることから左辺が計算できます。
U ( y ) − U ( 0 ) = 1 2 [ y d − ( y d ) 2 ] ε 0 S d V 2 (6)
U(y) - U(0) = \dfrac{1}{2} \left[ \dfrac{y}{d} - \left( \dfrac{y}{d} \right)^2 \right] \varepsilon_0 \dfrac{S}{d} V^2 \tag{6}
U ( y ) − U ( 0 ) = 2 1 [ d y − ( d y ) 2 ] ε 0 d S V 2 ( 6 )
K ( y ) − K ( 0 ) = 1 2 m v ( y ) 2 (7)
K(y) - K(0) = \dfrac{1}{2} m v(y)^2 \tag{7}
K ( y ) − K ( 0 ) = 2 1 m v ( y ) 2 ( 7 )
U g ( y ) − U g ( 0 ) = m g y (8)
U_g (y) - U_g(0) = mgy \tag{8}
U g ( y ) − U g ( 0 ) = m g y ( 8 )
また,導体極板が距離 0 0 0 y y y − q u − ( − Q ) = Q − q u = q d -q_u - (-Q) = Q - q_u = q_d − q u − ( − Q ) = Q − q u = q d
W V ( y ) = q d V = y d ε 0 S d V 2 (9)
\begin{aligned}
W_V (y) &= q_d V \\
&= \dfrac{y}{d} \varepsilon_0 \dfrac{S}{d} V^2 \tag{9}
\end{aligned}
W V ( y ) = q d V = d y ε 0 d S V 2 ( 9 )
(6) 〜 (9) 式を (5) 式に代入して v ( y ) v(y) v ( y )
1 2 m v ( y ) 2 = 1 2 [ y d + ( y d ) 2 ] ε 0 S d V 2 − m g y
\dfrac{1}{2} m v(y)^2 = \dfrac{1}{2} \left[ \dfrac{y}{d} + \left( \dfrac{y}{d} \right)^2 \right] \varepsilon_0 \dfrac{S}{d} V^2 - mgy
2 1 m v ( y ) 2 = 2 1 [ d y + ( d y ) 2 ] ε 0 d S V 2 − m g y
∴ v ( y ) = [ y d + ( y d ) 2 ] ε 0 S V 2 m d − 2 g y (10)
\therefore v(y) = \sqrt{\left[ \dfrac{y}{d} + \left( \dfrac{y}{d} \right)^2 \right] \dfrac{\varepsilon_0 S V^2}{md} - 2gy} \tag{10}
∴ v ( y ) = [ d y + ( d y ) 2 ] m d ε 0 S V 2 − 2 g y ( 10 )
として求められます。
V V V 導体円板が浮上を始めるような V V V
導体円板が浮上を始めるためには,0 ≤ y ≤ d 0 \leq y \leq d 0 ≤ y ≤ d v ( y ) v(y) v ( y ) 0 0 0 0 0 0 実数解の意味・二次方程式の実数解の個数 などをご覧ください。
y d = t ( 0 ≤ t ≤ 1 ) \dfrac{y}{d} = t \, (0 \leq t \leq 1) d y = t ( 0 ≤ t ≤ 1 ) f ( t ) f(t) f ( t )
f ( t ) = [ y d + ( y d ) 2 ] ε 0 S V 2 m d − 2 g d y d = ε 0 S V 2 m d t ( 1 + t ) − 2 g d t
\begin{aligned}
f(t) &= \left[ \dfrac{y}{d} + \left( \dfrac{y}{d} \right)^2 \right] \dfrac{\varepsilon_0 S V^2}{md} - 2gd \dfrac{y}{d} \\
&= \dfrac{\varepsilon_0 S V^2}{md} t (1 + t) - 2gd t
\end{aligned}
f ( t ) = [ d y + ( d y ) 2 ] m d ε 0 S V 2 − 2 g d d y = m d ε 0 S V 2 t ( 1 + t ) − 2 g d t
簡単のため a = ε 0 S V 2 m d , b = 2 g d a = \dfrac{\varepsilon_0 S V^2}{md}, b = 2gd a = m d ε 0 S V 2 , b = 2 g d a > 0 , b > 0 a > 0, b > 0 a > 0 , b > 0
f ( t ) = a t [ t − ( b a − 1 ) ]
f(t) = at \left[ t - \left( \dfrac{b}{a} - 1 \right) \right]
f ( t ) = a t [ t − ( a b − 1 ) ]
a > 0 , f ( 0 ) = 0 a > 0, f(0) = 0 a > 0 , f ( 0 ) = 0 0 ≤ t ≤ 1 0 \leq t \leq 1 0 ≤ t ≤ 1 f ( t ) ≥ 0 f(t) \geq 0 f ( t ) ≥ 0
b a − 1 ≤ 0
\dfrac{b}{a} - 1 \leq 0
a b − 1 ≤ 0
が成り立てばよいことがわかります。V V V
V ≥ 2 m g ε 0 S d
V \geq \sqrt{2 \dfrac{mg}{\varepsilon_0 S}} d
V ≥ 2 ε 0 S m g d
となります。
この関係が成り立っているとき,0 ≤ t ≤ 1 0 \leq t \leq 1 0 ≤ t ≤ 1 f ( y ) f(y) f ( y ) v ( y ) v(y) v ( y )
(f)
電流計を流れる電流 I I I Δ t \Delta t Δ t Δ Q \Delta Q Δ Q
I : = Δ Q Δ t
I := \dfrac{\Delta Q}{\Delta t}
I := Δ t Δ Q
として求められます (電場・磁場・電荷密度・電流密度|電磁気学における基本的な物理量 )。
y y y
I = Δ Q Δ t = Δ Q Δ y Δ y Δ t = Δ Q Δ y v ( y ) = q d y v ( y ) = ε 0 S V d 2 [ y d + ( y d ) 2 ] ε 0 S V 2 m d − 2 g y
\begin{aligned}
I &= \dfrac{\Delta Q}{\Delta t} \\
&= \dfrac{\Delta Q}{\Delta y} \dfrac{\Delta y}{\Delta t} \\
&= \dfrac{\Delta Q}{\Delta y} v(y) \\
&= \dfrac{q_d}{y} v (y) \\
&= \dfrac{\varepsilon_0 SV}{d^2} \sqrt{\left[ \dfrac{y}{d} + \left( \dfrac{y}{d} \right)^2 \right] \dfrac{\varepsilon_0 S V^2}{md} - 2gy}
\end{aligned}
I = Δ t Δ Q = Δ y Δ Q Δ t Δ y = Δ y Δ Q v ( y ) = y q d v ( y ) = d 2 ε 0 S V [ d y + ( d y ) 2 ] m d ε 0 S V 2 − 2 g y
と,y y y
(g)
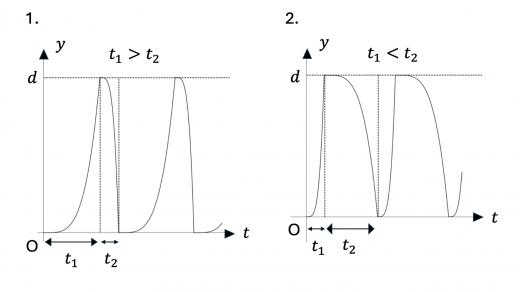
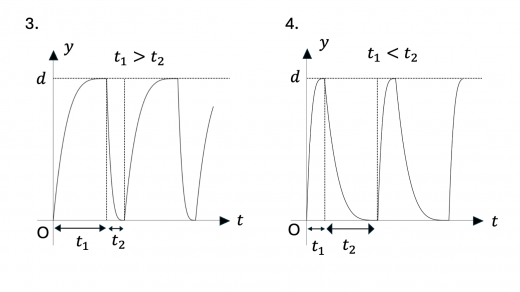
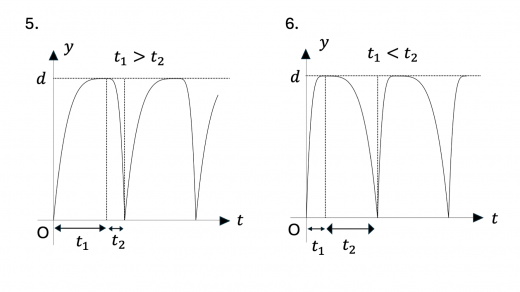
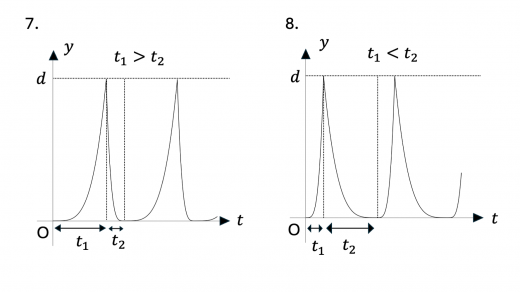
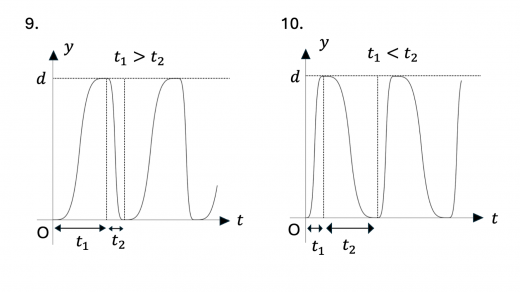
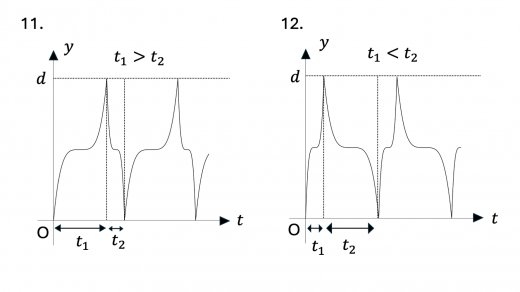
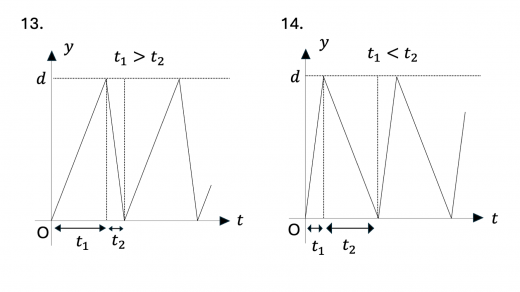
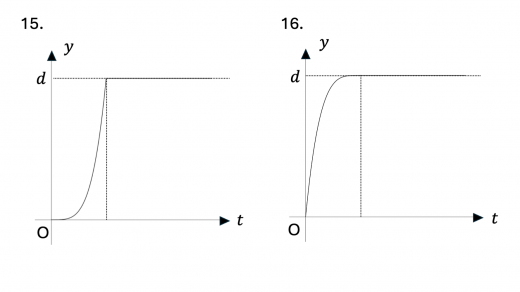
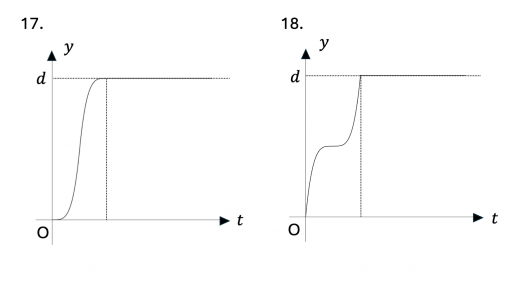
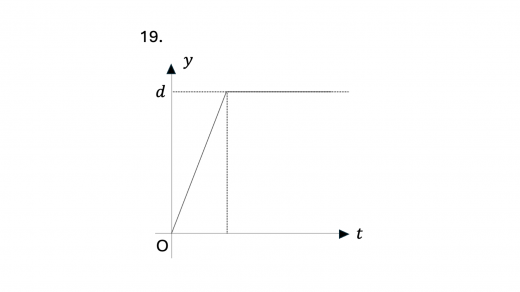
まず,0 < t < t 1 0 < t < t_1 0 < t < t 1 v v v y y y v v v y − t y-t y − t y y y d d d y − t y-t y − t 1.,2.,3.,8.,9.,10.,15. のいずれかとなります。
次に,y = d y = d y = d 弾性衝突(完全弾性衝突)の定義と性質 )をします。このとき導体円板の速度は急激に 0 0 0 y = d y = d y = d y − t y-t y − t 0 0 0 1.,2.,7.,8. となります。
さらに,上昇しきるのにかかる時間 t 1 t_1 t 1 t 2 t_2 t 2 下降にかかる時間の方が上昇のときにかかる時間より小さい,すなわち t 1 > t 2 t_1 > t_2 t 1 > t 2 と考えられます。上記のグラフのうちこの条件を満たすのは 1.,7. となります。
下降についてさらに考えてみます。初速度は 0 0 0 y y y 下降のときのグラフは,上昇時のグラフを上下反転させたようになり,上に凸になると考えられます 。この条件を満たすのは 1. のみとなり,これが求めるグラフになります。
コンデンサーの静電容量が C C C