【解答・解説】東大物理2025 第2問 -電磁気-
本記事中の図は全て,2025年度東京大学入試問題物理第2問を参考に,ライターが作成したものです。
I 図2-1のように,真空中に直径 ,長さ ,巻数 のソレノイド A がある。
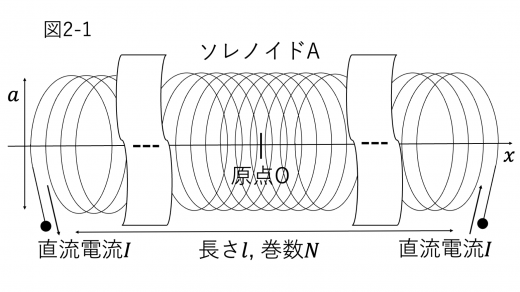 その中心軸を軸にとり,原点 O をソレノイド A の中心となるようにとった。軸は右向きを正とする。 は より十分に大きい。ソレノイド A に右から左に向けて一定の大きさ の直流電流を流す。真空の透磁率 (磁気定数) を として以下の設問に答えよ。
その中心軸を軸にとり,原点 O をソレノイド A の中心となるようにとった。軸は右向きを正とする。 は より十分に大きい。ソレノイド A に右から左に向けて一定の大きさ の直流電流を流す。真空の透磁率 (磁気定数) を として以下の設問に答えよ。
(1)原点 O での磁束密度の大きさ を求めよ。
(2)ソレノイド A を中央で二分割して左半分を取り除き,図2-2のように,右から左にかけて一定の大きさ の直流電流を流した。
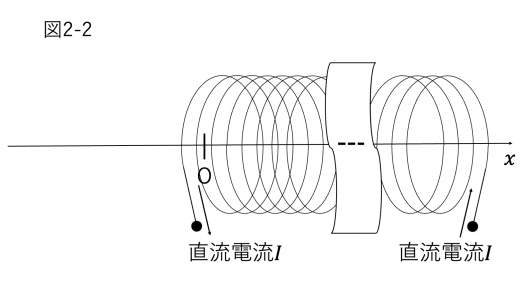
このとき,原点 O 付近の磁力線は図2-3のように表される。
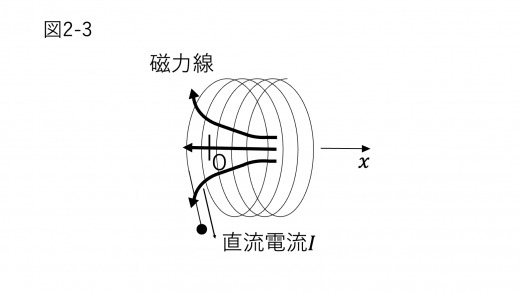
(上図の磁力線は概形です)
原点 O における磁束密度の大きさ を, を用いて表せ。
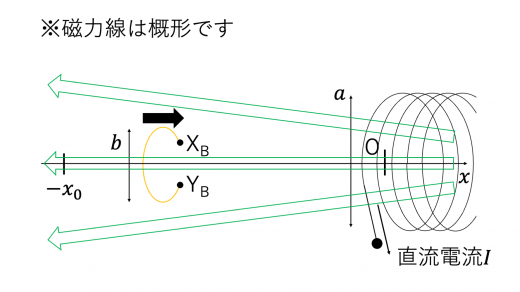
II 図2-4のように,設問 I(1) での長さ のソレノイド A を,中心軸が 軸,左端面中心が原点 O となるように固定し,右から左に向けて一定の大きさ の直流電流を流す。さらに,直径 ,巻数 1 の円形コイル B を,位置 からソレノイド A 内部の位置 まで等速運動させる。
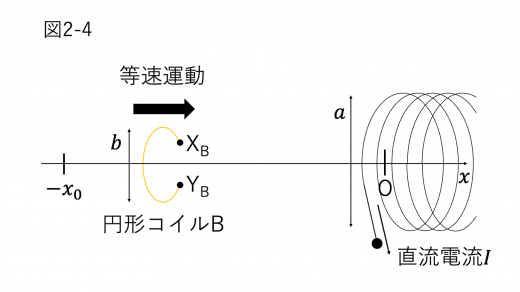
円形コイル B の中心は常に 軸上にあり,コイル面は 軸に垂直である。 は より十分に小さい。また,円形コイル B には紙面の手前側に端子 がある。その端子間距離は十分に小さく,円形コイル B の電気抵抗と自己インダクタンスは無視できる。
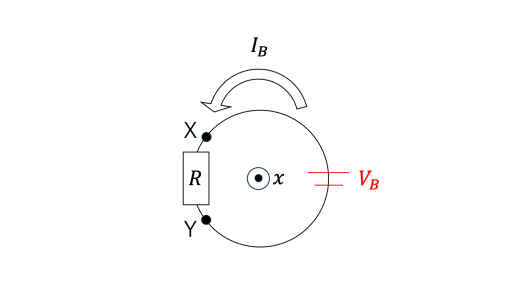
(1)端子 間に抵抗値 の電気抵抗を接続し,円形コイル B を等速運動させた。円形コイル B を貫く磁束が短い時間 の間に だけ変化したとき,円形コイル B に流れる電流の大きさ を求めよ。
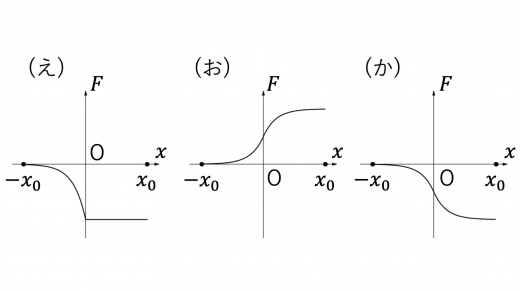
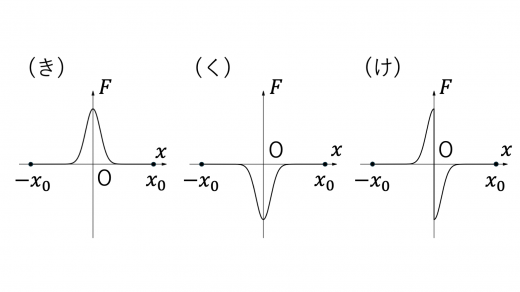
(2)円形コイル B 全体が磁場から受ける力を とする。 は右向きを正とする。前問 II(1) と同様に端子 間に抵抗値 の電気抵抗を接続し,円形コイル B を位置 から まで速さ で等速運動させたとき, と の関係を表すグラフの概形として最も適切なものを図2-5の (あ)~(し) から一つ選んで答えよ。
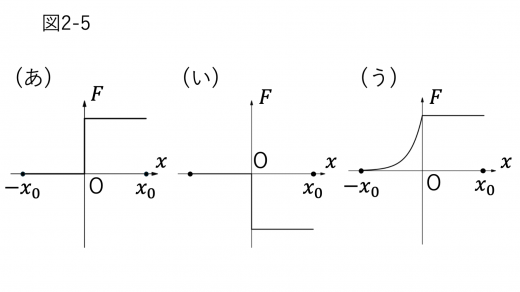
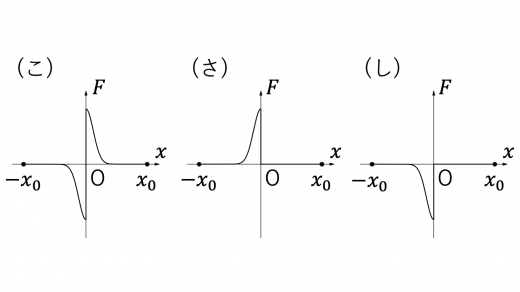
(3)前問 II(2) において,電気抵抗の抵抗値を から にすると, の大きさの最大値は何倍になるか,理由とともに答えよ。
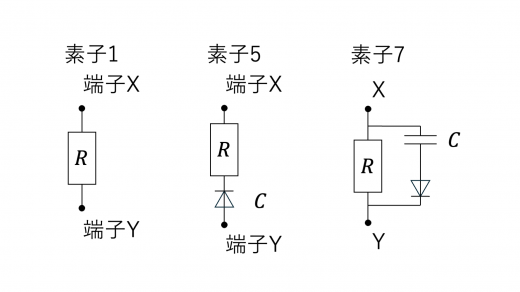
(4)図2-6に示す素子1~9は,抵抗値 の電気抵抗,電気容量 のコンデンサー,ダイオードからなる。
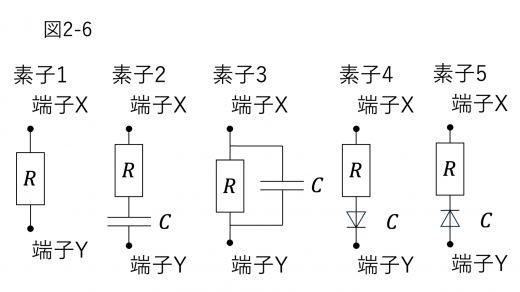
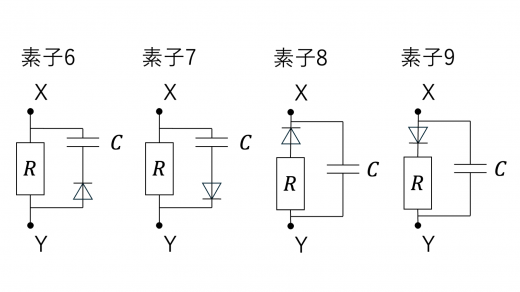
ダイオードでは,順方向には抵抗0で電流が流れ,逆方向には電流が流れないものとする。例えば素子4においては,紙面下向きに電流が流れ,上向には流れない。
ソレノイド A に流れる直流電流の向きを逆にし,左から右に向けて一定の大きさ の直流電流を流した。ここで,円形コイル B の端子 間に素子1~9のうち一つを選んで接続し,円形コイル B を位置 から まで速さ で等速運動させる場合を考える。ただし,円形コイル B の端子 に素子の端子 X を,端子 に素子の端子 を接続するものとする。このとき, と の関係が,設問II(2)と全く同じになる素子を図2-6の素子1~9からすべて選び,番号で答えよ。
III 図2-7のように,図2-4の状態からソレノイド A を取り除き,代わりに直径 ,巻数1の円形コイル C を固定した。
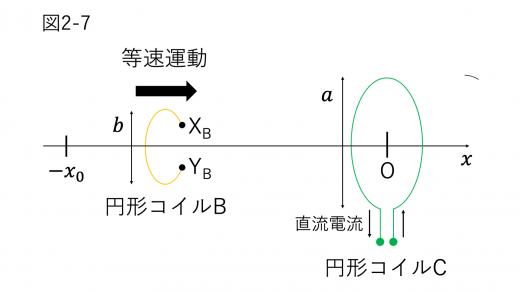
円形コイル C の中心は原点 に一致し,コイル面は 軸に垂直である。円形コイル C に一定の大きさの直流電流を,左から見て反時計回りに流して磁場を作る。円形コイル B の端子 間に抵抗値 の電気抵抗を接続し,円形コイル B を位置 から まで等速運動させる。
円形コイル B 全体が磁場から受ける力を とする。 は右向きを正とする。 と の関係を表すグラフの概形を描け。なお, の最大値や最小値,それらをとる の値を示す必要はない。
磁束密度やローレンツ力の向きについて定性的な理解をできているかが問われる問題です。
解答例
解答例
I
(1)
磁束密度 と磁場 の区別に注意してください。
単位長さあたり 回巻きのソレノイドに電流 が流れているとき,ソレノイドの中心に生じる磁場の大きさ は
となります。その向きは右ねじの法則により定まります。
いま,ソレノイド A の単位長さあたりの巻き数 は
であり,磁束密度と磁場とには の関係があることから,ソレノイド A が原点 O に作る磁束密度の大きさ は
のように求められます。
(2)
ソレノイドがその中心に作る磁場の大きさの公式は,ソレノイド表面には適応できません。系の対称性を利用して求めます。
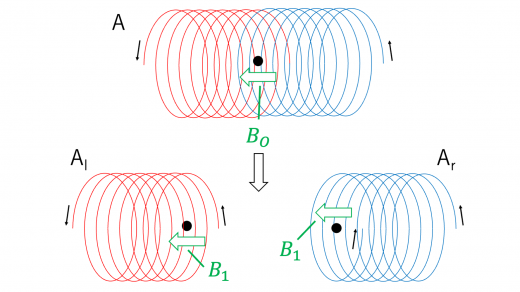
上図のように,ソレノイド A をその中心で に2等分することを考えます。ソレノイド がその表面で作る磁場および磁束密度は同じ分布を作ります。磁場および磁束密度の向きを考えると,対称性により
と求められます。
II
(1)
ファラデーの電磁誘導の法則 (電磁誘導とレンツの法則) より,コイル内の磁束密度の変化がコイルにもたらす誘導起電力の大きさ は
したがって,円形コイル B でキルヒホッフ第2法則を考えることで
と求められます。
(2)
まず, での のふるまいを考えてみます。
上図のように, 軸負方向に磁束密度は生じています。いま, 軸正方向に少し進んだとき,コイル B 内では 軸負の向きの磁束密度(および磁場)が増えます。したがって,ファラデーの電磁誘導の法則およびレンツの法則により, 軸正方向に磁束を増やす向きに誘導起電力および電流が流れます。
このときコイル B には下図のように電流および外部の磁場が生じます。
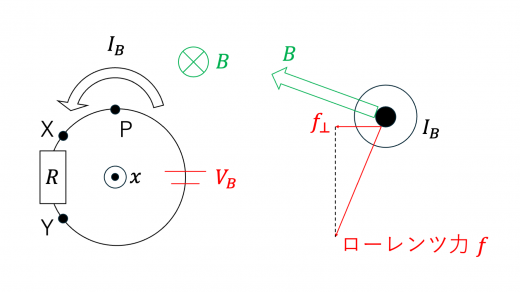
点 P にはたらくローレンツ力を考えてみます。コイル B は自身がつくる磁場の影響を受けないことを考えると,点 P にはたらくローレンツ力の向きは上図のようになります。コイル B の対称性により,ローレンツ力の 軸に垂直な方向の成分は打ち消しあうため,コイル B が受けるローレンツ力は 軸負の方向になります。これより(え),(か),(く),(こ),(し)が解答の候補として残ります。
次に, での のふるまいを考えます。 が原点より十分離れているとき,コイル B が 軸正方向に少し進んでも,コイル B 内を通過する磁束の大きさはほとんど変化しません。これより,ファラデーの電磁誘導の法則よりコイル B にはたらく誘導起電力の大きさも非常に小さい値となり0に収束します。これより(く),(こ),(し)が解答の候補として残ります。
(く),(こ),(し)を区別するためには,原点付近(特に正の領域)でどのような力が生じるかを考える必要があります。
で原点周辺を考えてみます。Iより原点では大きさ の磁束密度が 軸負の方向にはたらいています。ソレノイドの中に十分入ると,そこでの磁束密度は大きさ であり,向きは 軸正の方向となります。したがって,原点から の正の方向に少しだけ進むと,磁束密度は向きが 軸負の向きのまま,大きさが から少しだけ大きくなります。コイル内の磁束密度の変化の仕方は のときと同じなので, 軸負の方向に が生じます。これを満たすのは(く)のみとなります。
したがって,条件に合致するグラフの概形は(く)となります。
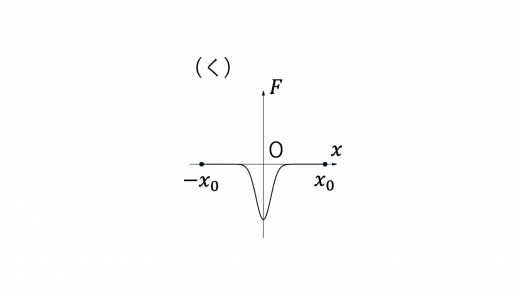
(3)コイル B 全体が磁場から受ける力 は,コイル B の各点に作用するローレンツ力 の合力として定まります。いま であるので, です。
II(1)より なので, となります。したがって,電気抵抗の抵抗値を から にすると, の大きさの最大値は 倍となります。
(4)II(2)とはソレノイド A に流れる電流の向きが逆になっているので,ソレノイド A が作る磁束密度の向きもII(2)とは逆の, 軸正方向となります。
素子 1 をコイル B に接続してみましょう。回路としてのコイル B はII(2)と同じ状態になっています。このとき,ファラデーの電磁誘導の法則およびレンツの法則により, の向きはII(2)と逆になります。磁束密度の向きと電流の向きがどちらも逆になるので,コイル B が受ける力 の向きおよび大きさはII(2)と全く同じになります。
したがって,素子 1 は条件を満たすことがわかります。また,これより,以下の条件を満たす場合, と の関係はII(2)と全く同じものになります。
・(*)電流がII(2)と逆向きに,II(2)と同じ回路素子のみを持つ回路を流れる
1つずつ順に検討していきます。
-
素子2:電流の流れる向きはII(2)と逆向きですが,回路は抵抗とコンデンサーから構成されており,どちらも への寄与があるため,条件(*)を満たしません。
-
素子3:素子2と同様の理由で条件(*)を満たしません。
-
素子4:回路が持つ素子はII(2)と同様に抵抗だけですが,ダイオードの作用により電流の流れる向きはII(2)と同じ向きとなるので,条件(*)を満たしません。
-
素子5:ダイオードのはたらきにより,条件(*)が満たされます。
-
素子6:並列回路に電流がどのように流れるかを考えます。まず,X → Y の方向に電流が流れる場合は,電流は抵抗のみからなる回路を流れますが,流れる向きはII(2)と同じ向きとなるので,条件(*)を満たしません。次に,Y → X の方向に電流が流れる場合は,流れる向きはII(2)と逆向きですが,ダイオードのはたらきにより電流は抵抗とコンデンサーの両方に流れるため,条件(*)を満たしません。次に,Y
-
素子7:電流が Y → X に流れる場合,条件(*)が満たされます。
-
素子8,9:素子6と同様の場合分けにより,電流の流れる方向がいずれの場合でも,条件(*)は満たされません。
したがって,条件を満たす素子は1, 5, 7となります。
III
円形コイル C が作る磁束密度の大きさおよび向きは,位置 の偶関数となっていることに注意してください。
コイル C が作る磁場の磁力線は下図のように書くことができます。
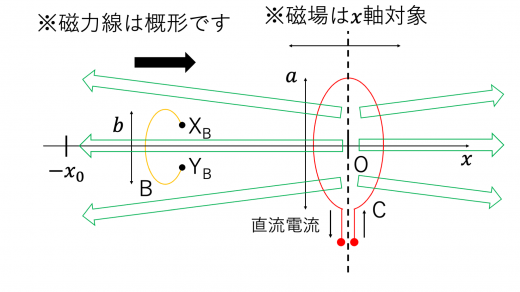
コイル C に十分近い場所 ( を正の数として )では,中心以外を通る磁力線もほぼ平行とみなすことができます。 より,この場所ではコイル B を貫く磁束がほぼ変化しないことになります。
のときを考えます。このとき, に近づくにつれて,コイル B を貫く 軸負の方向の磁束が大きくなり,それに伴ってコイル B には 軸負の方向の力 がはたらきます。 において の大きさは最大となります。 ではコイル B を貫く磁束密度の変化は徐々に小さくなるため, の大きさも徐々に小さくなっていき, で となります。
のときを考えます。コイル C が作る磁束密度の大きさおよび向きは位置 の偶関数となっていることより, も の偶関数となります。したがって, と の関係を表すグラフの概形は下図のようになります。
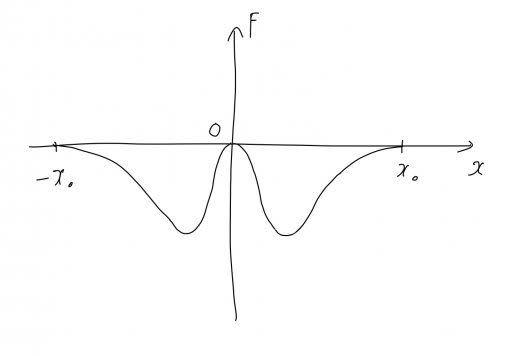
コイルやソレノイドが作る磁場の定性的な性質の理解が求められる問題です。計算量自体は少ないのですが,根拠を持って解を選ぶことは難しい問題です。











