電位差計

電位差計とは，電池の未知の起電力を測定するための装置です。回路図では，たとえば以下のように表されます。

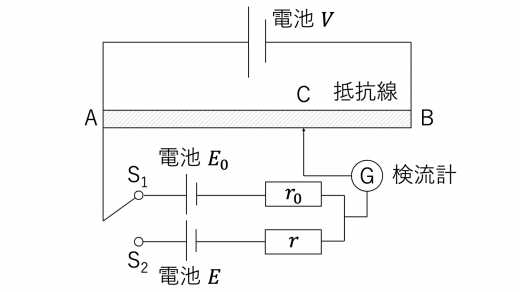
AB間には一様な抵抗線が挿入されており，長さ $L$，全体で抵抗値 $R_{AB}$ であるとします。

また，電池 $E_0, E$ の右に書かれている抵抗は，それぞれの内部抵抗で，抵抗値は $r_0, r$ であるとします。

検流計とは微小な電流の大きさと向きを測定する装置です。主に，検流計を電流が流れているかどうかを判別するのに用います。検流計の針の位置はCで表されています。

いま，既知の起電力 $E_0$ を持つ電池(標準電池とも言います)を用いて，未知の起電力を持つ電池の起電力 $E$ を求めてみましょう。

未知の起電力を求める

ステップ1

まず，スイッチS1をオンにし，スイッチS2をオフにします。

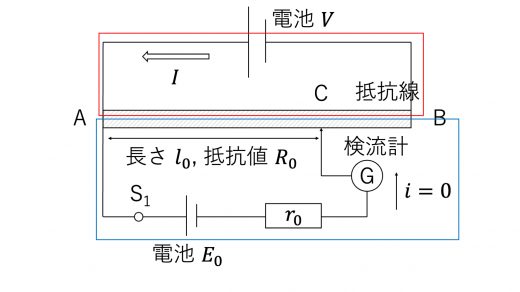
検流計の針を動かしたとき，$\text{AC} = l_0$ で検流計の針が0を示したとします。このときのAC間の抵抗が $R_0$ であるとすると，上図の赤線内および青線内において，キルヒホッフの第一・第二法則より(詳しくは キルヒホッフの法則の解説と例題 を参照)

$$V = R_{AB} I \tag{1}$$

$$E_0 = R_0 I \tag{2}$$

が成り立ちます。

ステップ2

次に，スイッチS1をオフにし，スイッチS2をオンにします。

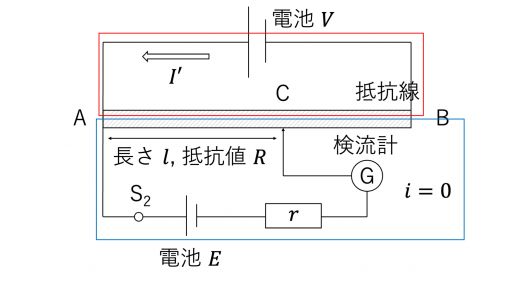
このとき，再び検流計の針を動かして，$\text{AC} = l$ で検流計の針が0を示したとします。

一様な抵抗率 $\rho$ を持つ，長さ $l$，底面積 $S$ の抵抗の抵抗値 $R(l, S)$ は

$$R(l, S) = \rho \dfrac{l}{S}$$

と表されたのでした。(詳しくは，オームの法則と抵抗の性質 を参照) これより，抵抗率と底面積が同じとき，抵抗値は抵抗の長さに比例していることがわかります。よって，AC間の抵抗値 $R$ は，ステップ1の $R_0$ を用いて

$$R = \dfrac{l}{l_0} R_0$$

と表すことができます。

いま，回路上部の電池(起電力 $V$)は共通なので，検流計の針が0のとき，抵抗線を流れる電流の大きさ $I'$ は，上図赤線内でキルヒホッフの第二法則より

$$V = R I' \tag{3}$$

と表されます。(1)・(3)式より，$I' = I$ であるとわかります。

また，上図青線内でキルヒホッフ第一・第二法則より

$$E = R I = \dfrac{l}{l_0} R_0 I \tag{4}$$

(2)・(4)式より

$$\dfrac{E}{E_0} = \dfrac{l}{l_0}$$

$$\therefore E = \dfrac{l}{l_0} E_0$$

と求められます。未知の起電力を，既知の起電力の大きさを用いて表すことができました。

電位差計を用いるメリット

電位差計を用いるメリットは，未知の電池に電流を流すことなく起電力を求めることができるという点です。

電池の内部抵抗 の記事で説明されているように，電池は電流を流せば流すほど，電池の端子電圧が低下していくことが知られています。

しかし，電位差計を用いて上述のように測定することで，未知の電池に電流を流さないようにすることができるため，より正確に起電力を求めることが可能になります。

これは検流計を用いる理由にもなっています。未知の電池に流れる電流は，(流れたとしても)できるだけ弱いまま，0になるよう調整することが必要です。したがって，微弱な範囲で電流の測定が可能な検流計が役に立つというわけです。