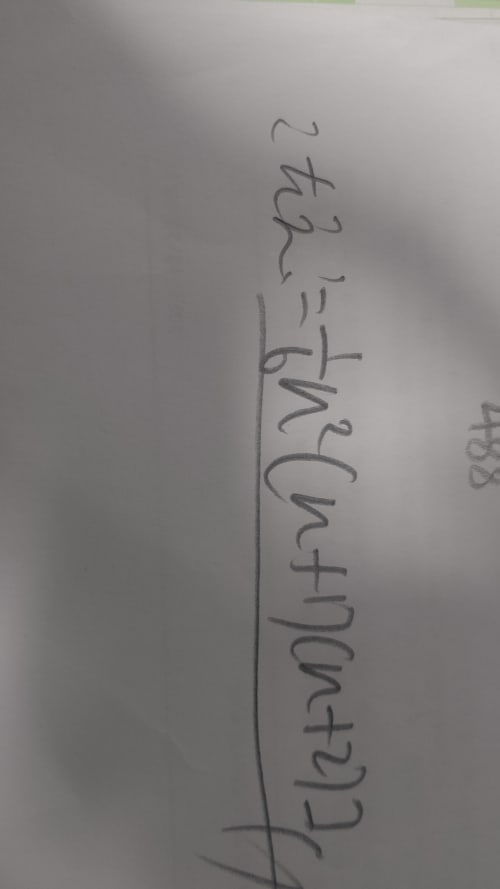数学A　場合の数と確率

投稿主様の求めている解答ではないかもしれませんが漸化式を使って解くことができたためそれを載せておきます。

$n$段のピラミッドの長方形と正方形の数の和を$a_n$とします。

$n+1$段のピラミッドは$n$段のピラミッドに比べ一番下に$2n+1$個ブロックが増えるためまず$1×(2n+1)$の長方形のみで出来る正方形と長方形を考えると

$1×1$の正方形が$2n+1$個、$1×2$の長方形が$2n$個、…$1×(2n+1)$の長方形が$1$個のためその合計は

$$(2n+1)+(2n)+…+1=\sum_{k=1}^{2n+1} k = \dfrac{1}{2} (2n+1)(2n+2)=(n+1)(2n+1)$$

となる。次に$n$段のピラミッドにあった正方形、長方形の内ピラミッドの底辺の一部を使っていたものは$n+1$段目が加わったことで高さ１マス分伸ばせるようになった（高さ１マス伸ばした四角形が増えた）。

これで増えた四角形は、$n$段のピラミッドにあった正方形、長方形の内ピラミッドの底辺の一部を使っていたものと同じ数だけありその数は、全体から底辺を使ってない四角形を引けばよいため$a_n-a_{n-1}$個あることがわかる。

上記二つに元々あった$a_n$を足したものが$a_{n+1}$であるから

$$a_{n+1}=(n+1)(2n+1)+(a_n-a_{n-1})+a_n , a_1=1,a_2=8$$

という漸化式ができ、これを$a_n$について解けばよい。

$a_{n+1}-a_n=(n+1)(2n+1)+(a_n-a_{n-1})$

$b_n=a_{n+1}-a_n,b_1=7$とすると

$b_n=b_{n-1}+(n+1)(2n+1)$より、

$b_n=b_1+\sum_{k=2}^{n} (k+1)(2k+1) =1+\sum_{k=1}^{n} (2k^2+3k+1)$

$=1+\frac{1}{3}n(n+1)(2n+1)+\frac{3}{2}n(n+1)+n$より

$a_{n+1}=a_n+1+\frac{1}{3}n(n+1)(2n+1)+\frac{3}{2}n(n+1)+n$

$n$に$n-1$をいれて

$a_{n}=a_{n-1}+\frac{1}{3}n(n-1)(2n-1)+\frac{3}{2}n(n-1)+n$より

$a_n=a_1+\sum_{k=2}^{n} \frac{1}{3}k(k-1)(2k-1)+\frac{3}{2}k(k-1)+k$

$=1+\frac{1}{6}\sum_{k=2}^{n} 4k^3+3k^2-k =\frac{1}{6}\sum_{k=1}^{n} 4k^3+3k^2-k$

$=\frac{1}{12}(2n^2(n+1)^2+n(n+1)(2n+1)-n(n+1))$

$=\frac{1}{12}n(n+1)(2n^2+2n+2n+1-1)=\frac{1}{6}n^2(n+1)(n+2)$