この問題を教えて欲しいです🙇🏻‍♀️‪‪´-

先ずは状況を整理して見ましょう。

問題文より、

$a_3=1$

$\displaystyle \sum_{k=1}^8 a_k=-10$

が分かりますね。

さて、この問題のポイントは何でしょうか？

この問題のポイントは${a_n}$が等差数列だと分かって居ると言うことです。

${a_n}$は等差数列なので初項を$\alpha$、公差を$d$と置くと、$a_n=\alpha+(n-1)d$と表せますね。

これを使うと、

第三項は

$a_3=\alpha+(3-1)d=\alpha+2d$、

初項から第八項までの和は

$\displaystyle \sum_{k=1}^8 a_k=\sum_{k=1}^8 \{\alpha+(k-1)d\}=\frac{1}{2} \cdot 8 \cdot \{\alpha+(\alpha+7d)\}=\frac{1}{2} \cdot 8 \cdot (2\alpha+7d)=8\alpha+28d$

（総和計算のところでは等差数列の和が$\frac{1}{2} \cdot 項数 \cdot (初項+第n項)$で表されることを使いました。いちいち分配法則を使って計算する必要がないのでお勧めですよ。）

これと先程問題文から読み取ったことを組み合わせると、

$\alpha+2d=1$

$8\alpha+28d=-10$

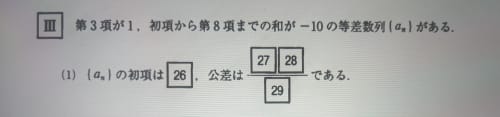
この連立方程式を解くと$\alpha=4,d=-\dfrac{3}{2}$が得られるので、初項は$4$、公差は$-\dfrac{3}{2}$だと分かります。