2017の東北大の問題で、複素数の方程式の解の個数について議論させる問題を解いている途中に疑問に思いました。
この問題は、虚数係数の方程式の解の個数なんぞ考えたことがない→実数を探して、いつも通りの方程式に帰着させる、と考えればすぐに解けるのですが、
虚数係数の方程式を一般に、考えることは不可能ですか?
この問題をなにも考えずに解いた(最初に自分が失敗)結果、右の写真の方程式を満たすzがちょうど2個あるための必要十分条件を求める必要があったのですが、ここから回答不能になりました。ここから回答を進めることはできますか?
学べることが1つあったのでもうお腹いっぱいですが、気になるのでお願いします!!

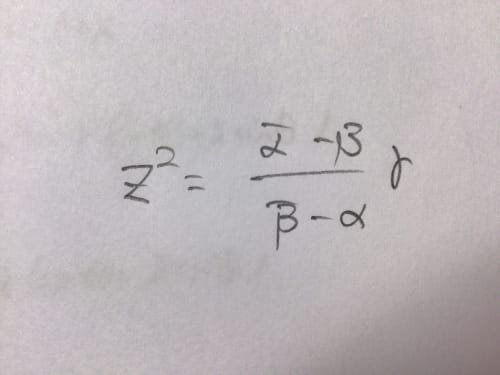
ベストアンサー

右の式の是非が僕には分からないので、「複素係数の一般方程式の解について複素数のままの形で考えることはできるか」という問いに一般化して答えます。
こと2次方程式に関して言えば、高校数学でも十分考えられると思います。
まず2次方程式の解の公式が複素数係数方程式に使えるか、
工夫すれば使えます。導出も実数係数と同じようにできるのでやってみてください。
複素係数方程式の解の公式は、
と書けます。
このとき、は平方根なので+と-の2個の値が入ると思ってください。複素数の乗は数Ⅲで習いますよね。
実数係数において判別式はでしたが、これも複素係数で使えます。
ただし、
重解なので解は個
解は個
となります。
3次方程式、4次方程式についても、解の公式が使えるので同様です。
また複素数係数の解の個数は、どれだけ重解があるかによって決まるので、微分することで求められる場合もあります。
なので、右の式の解の個数が2個になる条件は
になってしまうのかなと思います。
回答ありがとうございます!僕の方針でも回答可能なことがわかってよかったです!
そこで、記述の際はどのように書くのが適切でしょうか?
つまり、
を満たすzが2つ存在するための必要十分条件が、α≠0
であることはどう言えば良いですか?自明でもいいですかね?
あと、高校生の描く答案に、ルートの中に虚数が入るような答案ってアウトですかね?(実際自分もその処理をしらない)
>> を満たすzが2つ存在するための必要十分条件が、α≠0
であることはどう言えば良いですか?自明でもいいですかね?
このくらい直観的なら僕は自明でもいいと思っています。
学校で習ったやり方を使うなら、と置いて、においてはθが2つあり、ではの1つとなることを示すのが一番思い付きやすいですかね。
補足について
ルートの中に虚数は避けた方がいいでしょう、の定義はの平方根のうち以上の実数であるものです。
虚数の平方根は2つとも虚数になる(実数の2乗は実数であるの対偶)ので、本来は根号では書き表せません。
でも、結構いろんな場所で便宜上複素数にルートをかぶせる書き方が使われてるので、もしかしたら大学の先生方は見逃してくれるかも?
ここまで講釈をたれておいてなんですが、僕も質問者さんと同じように高3の受験生です。なので、自明非自明などは僕の肌感覚でしかないことはご了承ください。m(_ _)m
お互い頑張りましょう。









質問者からのお礼コメント
ありがとうございます。いろいろ知れて良かったです。
というかこのレベルの高三て、、、、離散か脅威しか思いつかないです笑、てかそうあって欲しいです🙏お互い頑張りましょう。