電磁気学のことでわからないことがあります。。。 (2)で、なぜ棒線部のところは成り立つのですか？また、こういうことを考

Question

電磁気学のことでわからないことがあります。。。

(2)で、なぜ棒線部のところは成り立つのですか？

また、こういうことを考えていると、平行板コンデンサーにおいても、どんな複雑な回路になっても2枚の極板の電荷の絶対値が同じになる理由がわからなくなったので、このこともできれば教えていただきたいです、、、

お願いします！！！！！

@atozkoxo · Accepted Answer

直観的には、『コンデンサーにおいて、1本の電気力線は1組の正電荷と負電荷で固定される』と理解すると良いと思います。そうすれば、もし片方の電荷が多いと、固定されない電気力線が存在することになるため気持ち悪いです。

$\underline{発展}$

より定量的な評価では、ガウスの法則（積分形）を用いるとよいでしょう。ガウスの法則とは、以下の式で書かれるものです。

$\int_S \bm{E}\cdot\bm{n}dS=\frac{Q}{\epsilon}$

左辺は、いわゆる面積分と呼ばれるものです。ある閉領域を包む平面について、その平面上の外向き単位法線ベクトルとその平面での点を始点にする電場ベクトルの内積をより集めたというイメージですね。https://www.px.tsukuba.ac.jp/~onoda/butsurib1/node7.html

の図1.8が視覚的に分かりやすいでしょう。

右辺の $Q$ は、その領域内の総電荷量です。 $\epsilon$ は誘電率です。つまり、『閉領域表面での電場が分かれば、その中にいる電荷量が分かる』という法則なわけですね。

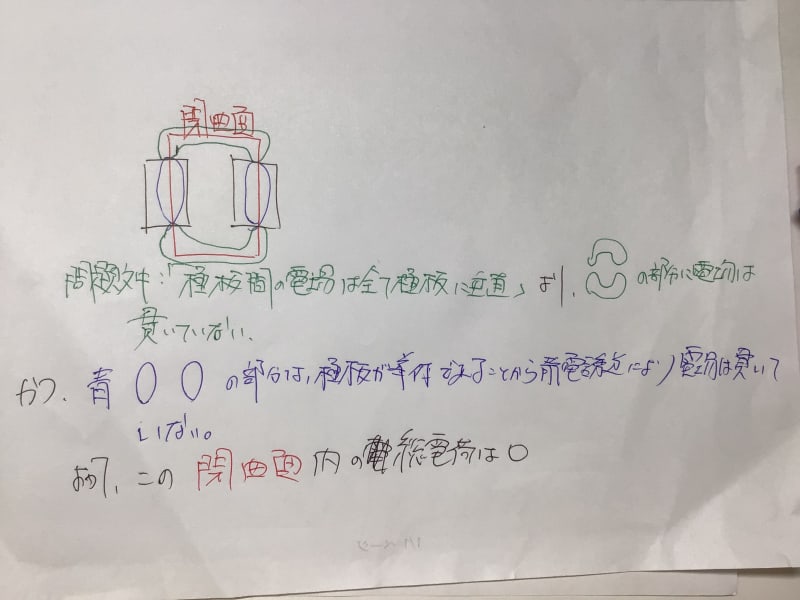
では、ここで閉領域を『極板AとBの隙間をすっぽり埋める領域』と思ってしまえばどうでしょう。AとBは平行なので、この領域は円筒か直方体になりますね。電場はAとBに直交する向きですから、結局内積の値が残るのは各極板の表面のみとなります。Aの表面に残る電荷量を $Q_1$ 、Bの表面に残る電荷量を $-Q^\prime_1$ としますと、ガウスの法則の右辺は