この解答（グラフ）になる理由を教えてくださいm(_ _)m

どこから説明すべきかわからないので、最初から説明していきます。

電位とは電気的な位置エネルギーのことを言いますが、簡単に言えば

「電荷量$q$をもつ電荷は距離$r$だけ離れた点に存在する粒子に

$$U=k\frac{q}{r}$$

という位置エネルギーを与える。」

ということです。この$U$を電位といいます。ちなみに、$r$は距離を表すので、$r>0$に注意してください。

次に、電位は重ね合わせられるということを覚えましょう。電位の重ね合わせは以下の様に記述されます。

「n個の荷電粒子が散在していて、それらがある位置に存在する粒子に与える電位$V$を考えると、各荷電粒子と対象粒子間の距離を$r_1,r_2,...r_n$として

$$V=k\frac{q_1}{r_1}+k\frac{q_2}{r_2}+...+k\frac{q_n}{r_n}=\Sigma_{i=1}^{n}k\frac{q_i}{r_i}$$

と書ける。」

なぜこのようなことが成り立つのか、というのは高校範囲で説明するのが大変なのでいったん省略します。とりあえず受け入れて下さい。さて、これらを頭に入れて解答を見ていきましょう。

$\underline{解答}$

位置$(x,0)$における電位$V$について考える。

$(a,0)$と$(x,0)$間の距離を$r_1$、$(-a,0)$と$(x,0)$間の距離を$r_2$とすると

$$r_1=|x-a|,\ r_2=|x+a|$$

と書ける。したがって

$$V=k\frac{Q}{|x-a|}+k\frac{(-Q)}{|x+a|}=k\frac{Q}{|x-a|}-k\frac{Q}{|x+a|}$$

グラフを書きやすいように場合分けしておく。

$\underline{x>aの場合}$

$$V=k\frac{Q}{x-a}-k\frac{Q}{x+a}=\frac{2kQa}{x^2-a^2}$$

$\underline{-a\leq x \leq aの場合}$

$$V=-k\frac{Q}{x-a}-k\frac{Q}{x+a}=-\frac{2kQx}{x^2-a^2}$$

$\underline{x<-aの場合}$

$$V=-k\frac{Q}{x-a}+k\frac{Q}{x+a}=-\frac{2kQa}{x^2-a^2}$$

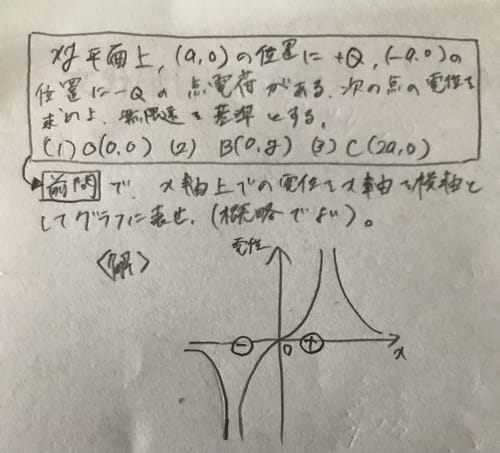
あとはこれらを愚直にグラフにしていけば解答の図を得る。特に、

$-a\leq x \leq a$の場合において、分母が負になっていることに注意すること。

（解答終）

補足：大学で物理を学ぶと、電場の重ね合わせが許される理由がなんとなくわかるようになります。（もちろん、高校でも直感的になんとなくわかる人もいますが、そこまで簡単な直感でもない気がします。）