暇つぶしに模試風のものを作ってみました。もし暇な方がいたら解いてみてください。感想も下さると嬉しいです。共通試験以降も数学を使う人たちが対象です。
普通~やや難ぐらいを目指しましたが、難易度感についてもコメントがあると参考になります。
(前にも似たようなことをやったのですが、その時よりは難しくしたつもりです。)
なお、大問3は千葉大学の改題です。
なお、大問5で「は非負の整数」となっていますが、正しくは「は正の整数」です。申し訳ありません。
既に回答してくれている方の返信欄は開かない方が良いと思います。ネタバレを食らいます。


ベストアンサー

私の実力不足のせいで1と2は完答出来なかったのですが、一応感想を載せたいと思います。
1よくある空間図形を平面で切って求積させる問題ですね。ただ今回の積分の形で示せというのが少しイレギュラーかなと思います。(少なくとも私の回答だとt以外の積分変数が出てしまいそうだったので。)それ以降は発想が及びませんでした。
2楕円の定義から方程式を出させるのは少し面倒とはいえ、シンプルな軌跡の問題と考えればそこまで難しいものでもないと思います。しかし、その後の極方程式への変換がうまくいきませんでした。それ以降は解いていません。(証明していないものを既知として使うのも居心地が悪いので)
3今回1番意図が読めなかった問題です。全体を通して全く難しいことを聞いていない気がしました。私が見えない落とし穴にはまっているのか、それとも難しい問題を改題した結果簡単になってしまったのか分かりませんが。
4他の問題と比べると割とポピュラーな問題なのではないかと思います。受験生で一度でも解いたことがある人であれば手が止まることはないでしょう。
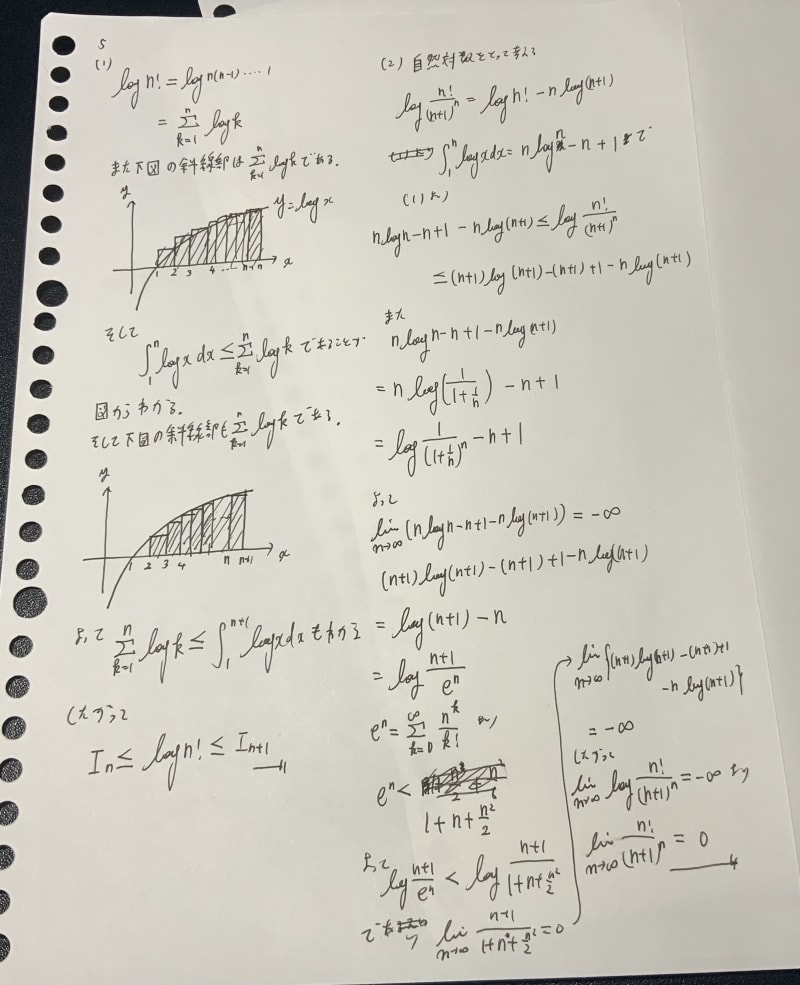
5これもよくある問題ですね。面積で不等式を評価するのは常套手段であり、本問ではそれ以上難しいことも聞いていないので気づいてしまえば完答できそうな問題ですね。
解いていただいてありがとうございます。(前回もあなたでしたね、本当にありがとうございます。)
一応、今回はあと数人に解いていただきたいなと考えていますので、一応ヒントと解いてあるものについてのコメントだけ載せます。
1について
今回で切断していると思いますが、他の平面で切ってみるのはどうでしょうか。そうすると、三角形を集めるような積分に帰着するはずです。(多変数関数の積分を許すなら、で切断したほうが良いのかもしれませんが、そこはまだ検討していません。)
2について
楕円の方程式から極形式を導こうとしたのかもしれません。それだと少し大変かもしれませんね。一応、楕円の定義をわざわざ書いてもらった意図として、「楕円の定義から出発したほうが楽かもね?」というメッセージだったりします。
3について
これは、正直想定してなかったですね。(笑)
恐らく改題したことによるエラーですね。本来ならば、因数分解などはせずに、定義した数列を用いて(3)を示してほしいと言うものでした。改題の下手さが出てますね。申し訳ない。
4について
完璧です。もはやコメントのしようがありません。
5について
ほぼ想定通りです。一応、こちらは(1)の不等式をダイレクトに指数的な書き方に直してしまう方法を用意していましたが、手間は変わらないように思います。