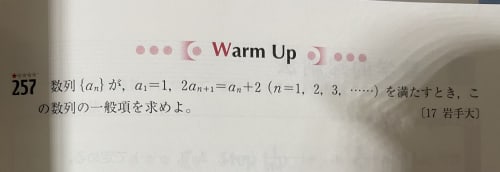この問題の解き方を教えて頂きたいです。

基本的なことからわからないということなので、隣接 $2$ 項間の漸化式から一般項を求める方法を原理から説明するので、以下長くなります。

まず、初項 $a_1=1$ を無視して漸化式 $2a_{n+1}=a_n+2 \quad \cdots (1)$ のみを考えます。

ここで、この漸化式を満たす数列が何か $1$ つ見つかったとします。この数列を $\{c_n\}$ とおくと、$2c_{n+1}=c_n+2 \quad \cdots (2)$ を満たします。

この数列は、漸化式さえ満たしていればどんな数列でも結構です。無限個存在します。詳細は後で述べます。

ここで、これら $(1),(2)$ の差をとると、

$$2(a_{n+1}-c_{n+1})=a_n-c_n \\ \iff a_{n+1}-c_{n+1}=\dfrac{1}{2}(a_n-c_n)$$

$a_n-c_n=b_n$ とおくと、$$b_{n+1}=\dfrac{1}{2}b_n$$となります。これは単純な等比数列ですね。公比は $\dfrac{1}{2}$ なので、初項さえ分かれば数列 $\{b_n\}$ の一般項は求められそうです。

ここで、数列 $\{c_n\}$ について考えてみましょう。この数列は漸化式さえ満たしていれば何でもよいのでしたね。では $2c_{n+1}=c_n+2$ を満たすもののうち、最も簡単なものは何でしょうか。

それは定数数列ですね(おそらく)。つまり、ずっと同じ値をとり続ける数列のことです。その値を $\alpha$ とすると、$2\alpha=\alpha+2 \iff \alpha=2$ となります。

このとき、$c_1=2$ であり、$b_1=a_1-c_1=-1$ です。

こうして $b_n=-\biggl(\dfrac{1}{2}\biggr)^{n-1}$ が求められ、

$$\begin{aligned}a_n&=b_n+c_n \\ &=2-\biggl(\dfrac{1}{2}\biggr)^{n-1}\end{aligned}$$

が得られます。

では、$\{c_n\}$ などという数列をいちいち考えなくても、はじめから $\alpha$ を考えるのはどうでしょうか。そちらの方がはやそうですよね。

ということで、数列の漸化式 $a_{n+1}=pa_n+q$ を解くアルゴリズムを以下にまとめて終了とします。

①漸化式 $a_{n+1}=pa_n+q$ を満たす特殊解 $\alpha$ を求める。

　→ $\alpha=p\alpha+q$

この①は解答に書く必要はありません。

②漸化式 $a_{n+1}=pa_n+q$ を $a_{n+1}-\alpha=p(a_n-\alpha)$ に変形

　→このとき、もとの漸化式に戻るか検証すること。

③数列 $\{a_n-\alpha\}$ は等比数列なので、その一般項を求める。$b_n=a_n-\alpha$ とおいてもよいが、おかなくても解けるくらいの計算力を身に付けたい。

④$a_n$ を求める。

あとは演習問題をたくさん解いて、完璧に理解していきましょう。