4×5マスの方眼紙において正方形の個数がいくつになるかという問題が分からないので解き方、何故そうなるのか理由も添えて教えていただけると幸いです。よろしくお願い致します_(._.)_

(正方形を方眼紙のマス目で構成されるという仮定で説明していきます)

とっつきにくいようにもみえるこの問題ですが、答えである正方形の大きさから考えてみるとすっきりします。つまり一辺の長さが$1,2,3...$となるような状況を考えるということです。早速場合分けしてみましょう

一マス分の長さを$n$とします

$(Ⅰ)n=1のとき$

$4×5の方眼紙ですからそのまま20$個の正方形がでるのは自明ですね

$(Ⅱ)n=2のとき$

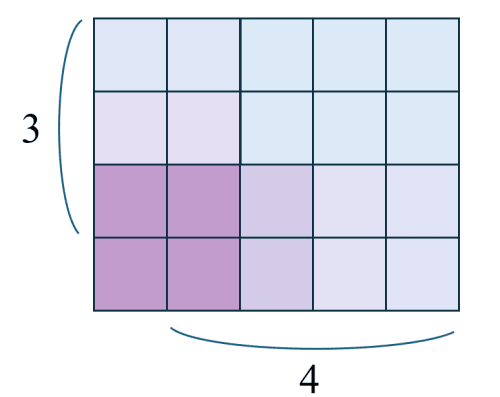
$2×2$の正方形を方眼紙の中で動かすイメージで見てみると、縦には3,横には4マスぶん自由に動けるのがわかります。例として画像を参照してみてください。

すると動ける分だけ正方形がありますから$3×4=12$個の正方形があります。

$(Ⅲ)n=3のとき$

上記と同様の考え方で大丈夫ですね。すると、動ける範囲は$縦2,横,3$であるので$2×3=6$個の正方形です。

$(Ⅳ)n=4のとき$

$動ける範囲は縦1,横2ですので2つしか正方形がありませんね。$

$(Ⅰ)～(Ⅳ)$を計上し、$20+12+6+2=40$

よってもとめる値は$40$となります。

ちなみに、

もしこれをもっともらしく書くならば

$$Ans.=\sum_{k=1}^{4} k(k+1)=\dfrac{4(4+1)(2・4+1)}{6}+\dfrac{4(4+1)}{2}=40$$

でしょうかね？これだと式にもちゃんと意味が付与されてます