京大実戦の数学で納得いかないことがあります、この問題、絶対に解ける問題だと思って最初、Vkを求めようとしましたが、三角形の形が鈍角三角形になることを全く証明できませんでした。というか本当に全てのkに対して鈍角三角形になるのかどうかも怪しく感じていました。
ですが模範解答を見ると鈍角三角形になることの証明はないみたいです。これは論証不足ではないのですか?参考書は河合塾のものです。
どう思いますか。意見をお願いいたします🤲
問題がみにくければ言ってください。すぐに載せます

ベストアンサー

鋭角三角形だとして考えてみましょう。
すると、回転体の高さの部分は、となりますね。底辺の長さということです。
鋭角三角形だろうと鈍角三角形だろうと、底辺を軸に回転させた場合、その体積は
となるわけです。
論証が気になるのならば場合わけして書いても良いと思いますが(その方が丁寧です。)、これは既知の事実だとして、鋭角・鈍角の片方のみの記述でも大丈夫だと判断して解答を作成したのではないでしょうか。(紙面の都合もありますし)
添付画像に詳しく書いてありますので、目を通していただけたら幸いです。
受験勉強頑張って!

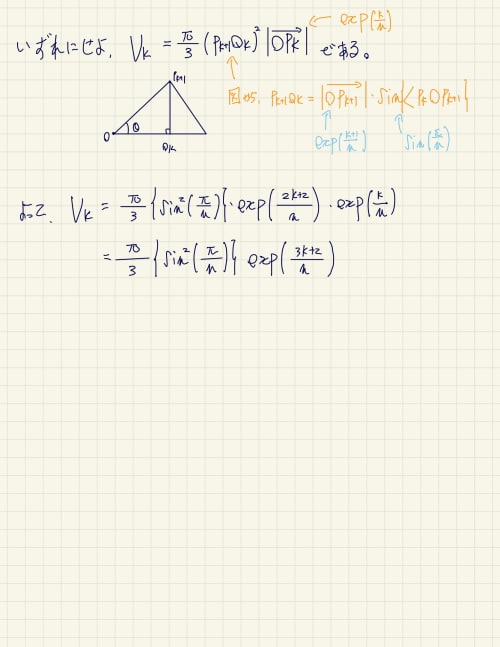









質問者からのお礼コメント
綺麗に納得しました。ありがとうございます。今度からはexp(k/n)とかの数式だけでなく、OPkのように表示して柔軟に考えていきたいと思います。