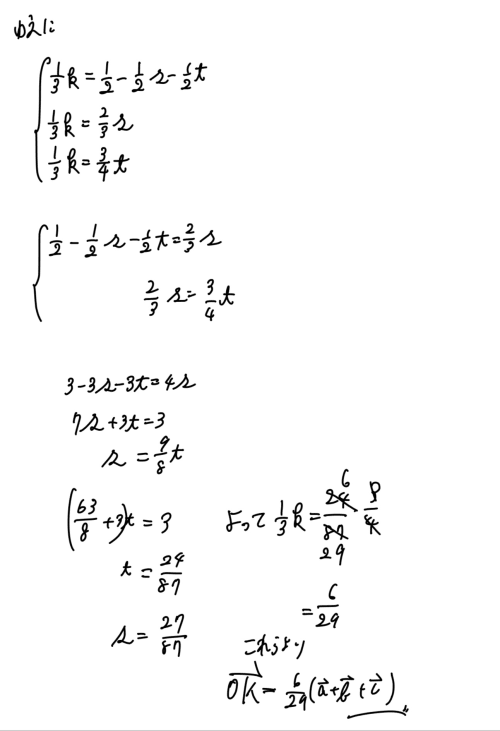• 解決済み

    @Rena_7643

    2022/7/11 17:39

    1 回答

    四面体OABC を考える。辺OAの中点をPとする。また辺 OBを2:1 に 内分 する点を Qとして,辺OC を3:1に内分する点をRとする。更に三角形ABCの重心をG とする。

    3点P,Q,R を通る平面と直線OGの交点をKとするとき, OKベクトルを OAベクトル, OBベクトル OCベクトルを用いて表せ。


    PKベクトル=sPQベクトル+tPRベクトル（s、tは実数）

    とおいてこの問題を解きたいんですが、

    途中式をお願いします。



    ちなみに答えは

    OKベクトル=6/29OAベクトル+6/29OBベクトル+6/29OCベクトルです。

    1. 高校生
    2. 数学
    3. 数学Ⅱ・B

    ベストアンサー

    ベストアンサー

    @PEMANOUS

    2022/7/12 10:38

    最後の方雑になってますけど、ただ連立方程式解いてるだけなんで。答え方は元に戻し忘れました。

    そのほかの回答（0件）

    関連する質問

    もっとみる