電気振動？の問題だと思います。この初期状態からコイルに流れる電流が最大となった瞬間、スイッチを閉じた。スイッチを閉じてからコイルに流れる電流が初めて0になるまでの時間を求めよ。 がわかりません。電流が最大になるまでの時間はわかります。ただのコンデンサーが直列なだけの典型的な電気振動回路なので。T/4でπ√{LC1C2/(C1+C2)}/2ですよね。

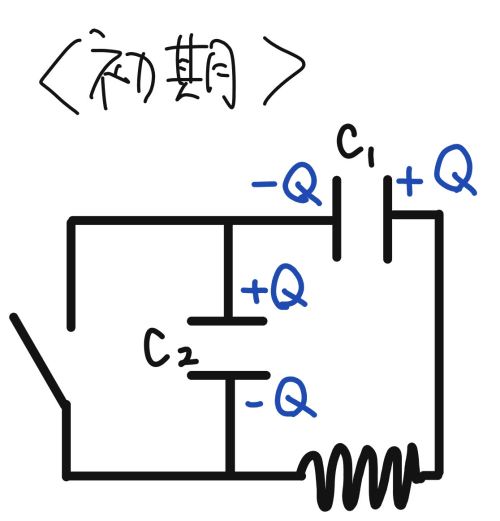
直観的な説明が難しかったので、数理的なところから説明します。微積分を使いますので、少し難しければ下線部のところを知識として押さえても良いと思います。

また、計算が煩雑な個所（6式や8式など）は計算を省略しています。興味があればご自分で手を動かしてみると良いかと思います。

まず、スイッチを入れる前について考えてみると、キルヒホッフの法則から

$$\begin{align}L\frac{dI}{dt}+\frac{C_1 + C_2}{C_1 C_2}Q_1=0\end{align}$$

が分かります。ここで、電流 $I$ はコイルを左から右に流れるように（つまり、半時計まわりに）定義しています。また、孤立部の電荷保存則から直ちに求まる $Q_1 = Q_2$ を適応しています。

さらに、電流の向きに注意すると、電流と電荷の関係は

$$\begin{align}\frac{dQ_1}{dt}=I\end{align}$$

で定められるため、(1)式を $t$ で微分した後(2)式を適用すると

$$\begin{align}\frac{d^2I}{dt^2}=-\frac{1}{L}\frac{C_1 + C_2}{C_1 C_2}I\end{align}$$

を得ます。これは単振動

$$\frac{d^2x}{dt^2} = -\omega^2 x$$

と同じ数理構造になっていることから

$$\begin{align}I(t) = A\sin \left(\sqrt{\frac{1}{L}\frac{C_1+C_2}{C_1 C_2}}t+\phi_0 \right)\end{align}$$

と書けることが分かります。振幅 $A\neq 0$, 初期位相 $\phi_0$ を初期条件から決定すること考えると、$Q_1(0)=Q,\ I(0) = 0$ なので

$$\begin{align}I(0) &= A\sin \phi_0 = 0 \Rightarrow \phi_0=0\\\left. L\frac{dI}{dt}\right|_{t=0} &= -\frac{C_1+C_2}{C_1 C_2}Q\Rightarrow A=-Q\sqrt{\frac{1}{L}\frac{C_1+C_2}{C_1 C_2}}\end{align}$$

と求まります。よって、$I(t)$ の表式は以下の様に求まりました。

$$\begin{align}I(t) = -Q\sqrt{\frac{1}{L}\frac{C_1+C_2}{C_1 C_2}}\sin \left(\sqrt{\frac{1}{L}\frac{C_1+C_2}{C_1 C_2}}t \right)\end{align}$$

ここで、$|I(t)|$ が最大になるような最小時刻を $t^*$ とおくと、

$$\sqrt{\frac{1}{L}\frac{C_1+C_2}{C_1 C_2}}t^*=\frac{\pi}{2}\Rightarrow t^* = \frac{\pi}{2}\sqrt{ \frac{L C_1 C_2}{C_1+C_2}}$$

と求まります。さらに、$t=t^*$ のときの電荷 $Q_1(t^*)$ を調べておくと

$$\begin{align}\left. L\frac{dI}{dt}\right|_{t=t^*} &= -\frac{C_1+C_2}{C_1 C_2}Q_1(t^*)\Rightarrow Q_1(t^*)=0\end{align}$$

が分かります。基本的に高校生が習うような範囲では、

$\underline{電気振動回路では、|I|が最大ならQ=0、|Q|が最大ならI=0}$

という関係が成り立ちます。（このような言い方をしているのは、特殊なセッティングのもとではそうならない可能性があるからです。実際に自分がその特殊なセッティングを知っているわけではありませんが。）

なお、この事実は(2)式から電荷を積分から求めることでも理解できます。

さて、問題の本論に移ります。ここでは、電流の大きさが最大となったタイミングを時刻0とし、時刻0で左側のスイッチを閉めたとしています。先程までの時刻と区別するために、ここでは時刻のラベルとして $t^{\prime}$ を採用します。

つまり、本論の初期条件として

$$\begin{align}Q_1(t^{\prime}=0)=Q_2(t^{\prime}=0)=0\\I(t^{\prime}=0) = -Q\sqrt{\frac{1}{L}\frac{C_1+C_2}{C_1 C_2}}\end{align}$$

が成り立ちます。左側のコンデンサ $C_2$ しかない閉回路を考えると、キルヒホッフの法則から

$$\frac{Q_2(t^{\prime})}{C_2}=0 \Rightarrow Q_2(t^{\prime})=0$$

すなわち $Q_2(t^{\prime})$ は時間に依存せず 0 であると分かります。

したがって、考えるべきキルヒホッフの法則は

$$\begin{align}L\frac{dI}{dt^{\prime}}+\frac{Q_1}{C_1}=0\end{align}$$

となり、これを初期条件(9), (10)式の基で考えればよいことになります。前半同様に (2)式が成り立ちますから、

$$\begin{align}\frac{d^2 I}{d{t^{\prime}}^2} &= -\frac{1}{LC_1}I \\\Rightarrow I(t^{\prime}) &= A^{\prime}\sin \left( \sqrt{ \frac{1}{LC_1} }t^{\prime} + \phi^{\prime}_0 \right) \end{align}$$

を得ます。ここで、(9)式と(11)式から、

$$\begin{align}\left. \frac{dI}{dt^{\prime}}\right|_{t^{\prime}=0} = A^{\prime}\sqrt{ \frac{1}{LC_1}}\cos \phi^{\prime}_0 = 0\\\Rightarrow \phi^{\prime}_0 = \frac{\pi}{2}\end{align}$$

すなわち、

$$\begin{align}I(t^{\prime}) &= A^{\prime}\cos \left( \sqrt{ \frac{1}{LC_1} }t^{\prime} \right) \end{align}$$

と分かります。したがって、電流が初めて0となる時刻を $\tau^*$ とすると

$$\sqrt{ \frac{1}{LC_1} }\tau^{*} = \frac{\pi}{2}\Rightarrow \tau^{*} = \frac{\pi \sqrt{LC_1}}{2}$$

と求めることが出来ます。なお、不要だったので$A^\prime$は求めていませんが、(10)式から求めることができます。

質問等あればお願いします。