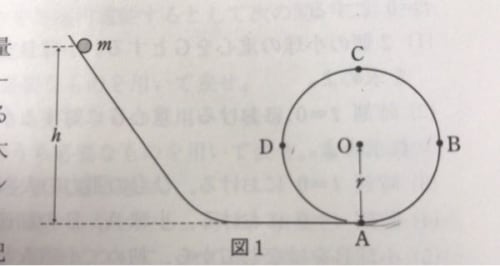
高校物理の円運動について質問です。

質問の内容を履き違えていたようです。申し訳ありません。（先程の回答は削除させて頂きました。）

結論から言えば、最高点以降は小球の速さが大きくなる一方だから大丈夫、ということになります。

今、小球に乗って動く観測者から見た場合を考えてみましょう。当然、これは非慣性系ですから、慣性力が乗ることになります。今回は円運動による慣性力が乗ることになり、これを「遠心力」と呼びます。

重力による円運動への寄与（つまり、重力の球の中心に向かう成分）を$W^{\prime}$とすると、観測者から見た力のつり合いの式は

$$m\frac{v^2}{r}=N+W^{\prime}$$

と書けます。なお、これを$N=$に直すと

$$N=m\frac{v^2}{r}-W^\prime$$

となります。この$N$が0にならない条件を探ればいいわけですね。

ところで、円軌道中で最も速さが遅くなる点は最高点です。（これは、例えばエネルギー保存則などから理解できると思います。）

また、$W^\prime$は最高点で最大になります。（図を書いてみると分かりやすいと思います。）

つまり、最高点において「遠心力」は最小であり、「$W^\prime$」は最大なので、$N$は最小になってしまいます。

したがって、

『最高点で$N\geq0$ならば、円軌道中のあらゆる点で$N\geq0$が満たされる』

という結論を得ることが出来ます。