1年解けずに放置した漸化式なのですが、どなたかご教授いだだけないでしょうか？

　あまり良い解き方か分かりませんが、下のようにすれば一応解は求まります。

　ひとまず $h(n + 1) = h(n)^2$ の形の漸化式を考察する。この漸化式を見て分かるのは、$h(n)$ の発散が $n!$ より速い（つまり大変速い）ことである。そこで両辺の対数をとって微分してみると

$$\frac{h'(n + 1)}{h(n + 1)} = 2 \frac{h'(n)}{h(n)}$$

を得る。ここで $H(n) = h'(n)/h(n)$ とおく。$H(n + 1) = 2 H(n)$ から容易に $H(n) = 2^{n - 1}H(1)$ が得られ、したがって

$$\frac{h'(n)}{h(n)} = 2^{n - 1} H(1)$$

を得る。これを形式的に未知関数 $h(n)$ の微分方程式と見なして解けば、

$$h(n) = C \exp\left(\frac{H(1)}{\log 2} 2^{n - 1}\right)$$

を得る（ここで $C$ は任意定数）。これを元の方程式 $h(n + 1) = h(n)^2$ へ代入してみると、$C = 1$ でなければならないと分かる。また $H(1)/\log 2$ は定数であるからこれを $A$ とおく。すると最終的に

$$h(n) = \exp(A 2^{n - 1})$$

を得る。これが漸化式 $h(n + 1) = h(n)^2$ のすべての解の表現である。

　$h(n + 1) = h(n)^2$ の $2$ つの解 $h_1, h_2$ をとる。$h_3(n) = h_1(n) + h_2(n)$ とおくと

$$\begin{aligned}h_3(n + 1) &= h_1(n + 1) + h_2(n + 1) \\ &= h_1(n)^2 + h_2(n)^2 \\ &= (h_1(n) + h_2(n))^2 - 2 h_1(n) h_2(n) \\ &= h_3(n)^2 - 2 h_1(n) h_2(n)\end{aligned}$$

となる。ここでもし $h_1(n), h_2(n)$ を適切に選ぶことで $h_1(n) h_2(n) = 1$ とできるならば、$h_3$ は、漸化式 $g(n + 1) = g(n)^2 - 2$ の解となる。そこで $h_1(n) = \exp(A_1 2^{n - 1}),\ h_2(n) = \exp(A_2 2^{n - 1})$　として、

$$h_1(n) h_2(n) = \exp(2^{n - 1} (A_1 + A_2)) = 1$$

という方程式を立てる。この方程式が成り立つ必要十分条件はあきらかに $A_1 + A_2 = 0$ の成立である。この条件を満たす $A_1, A_2$ はあきらかに存在する。よって、$g(n + 1) = g(n)^2 - 2$ の解は、$h(n + 1) = h(n)^2$ の $2$ つの解の和として表わされると分かる。

　あとは $g(1) = 3$ という条件を満たすように $A_1 = -A_2$ の値を定めればよい。これを定めるには

$$\exp(A_1) + \exp(A_2) = 3$$

を解く。$A_1 = \log x$ とおけば、これは $x^2 - 3x + 1 = 0$ を解くことに等しい。これを解いて

$$A_1 = \log \frac{3 + \sqrt{5}}{2} = \log \phi^2$$

を得る。（ここで $\phi = (1 + \sqrt{5})/2$）

　以上の結果をまとめれば、$g(n + 1) = g(n)^2 - 2,\ g(1) = 3$ の一般項は

$$g(n) = \phi^{-2^n} + \phi^{2^n}$$

となる。

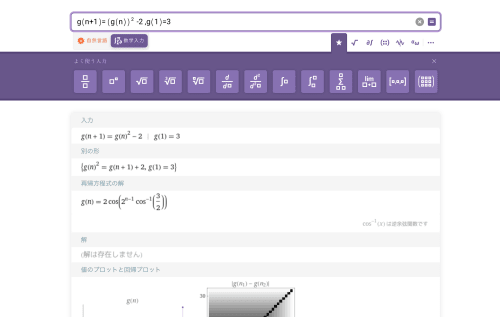
※ $\arccos$ の引数に $1$ より大きい数が与えられているのは、$\arccos$ を複素関数として扱っているからです。複素関数を使った Wolfram の表現も黄金比 $\phi$ を使った上の表現も同じものです。