下の問題の解法をご教示ください。

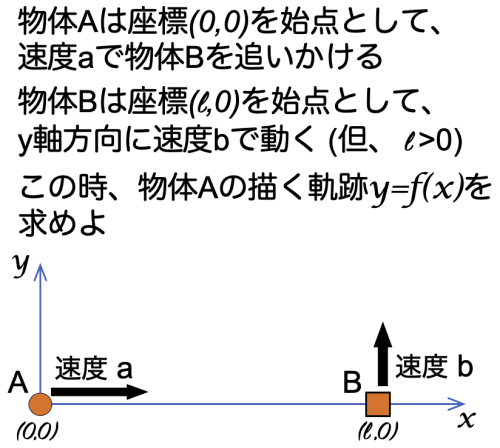
時刻 $t$ におけるAの座標を $(x,y)$ とする。

さらにAの速度を

$$\overrightarrow{a} = (a_x, a_y) = \left(\dfrac{dx}{dt}, \dfrac{dy}{dt}\right)$$

とする。

AはBに向かって進むので、Aの速度の接線方向にBがいる。

さらに時刻 $t$ におけるBの座標は $(\ell, bt)$ であるから、

$$\dfrac{a_y}{a_x} = \dfrac{dy}{dx} = \dfrac{bt - y}{\ell - x}$$

が成り立つ。

これを変形し、両辺を $t$ で微分して整理を進めていく。

$$\{\ell - x(t) \}\dfrac{dy}{dx} = bt - y(t) \\\dfrac{d^2y}{dx^2} = \dfrac{b}{(\ell - x)\dfrac{dx}{dt}}$$

ここから $t$ を消去したい。ここで

$$\begin{aligned}a^2 &= a_x^2 + a_y^2 \\a &= \dfrac{dx}{dt} \sqrt{1 + \left( \dfrac{dy}{dx} \right)^2 }\end{aligned}$$

であるから、

$$\dfrac{d^2y}{dx^2} = \dfrac{b}{(\ell - x)a}\sqrt{1 + \left( \dfrac{dy}{dx} \right)^2 }$$

が成り立つ。

あとはこの微分方程式を初期条件 $x(0) = 0, y(0) = 0$ を用いて解けば良いと思います。