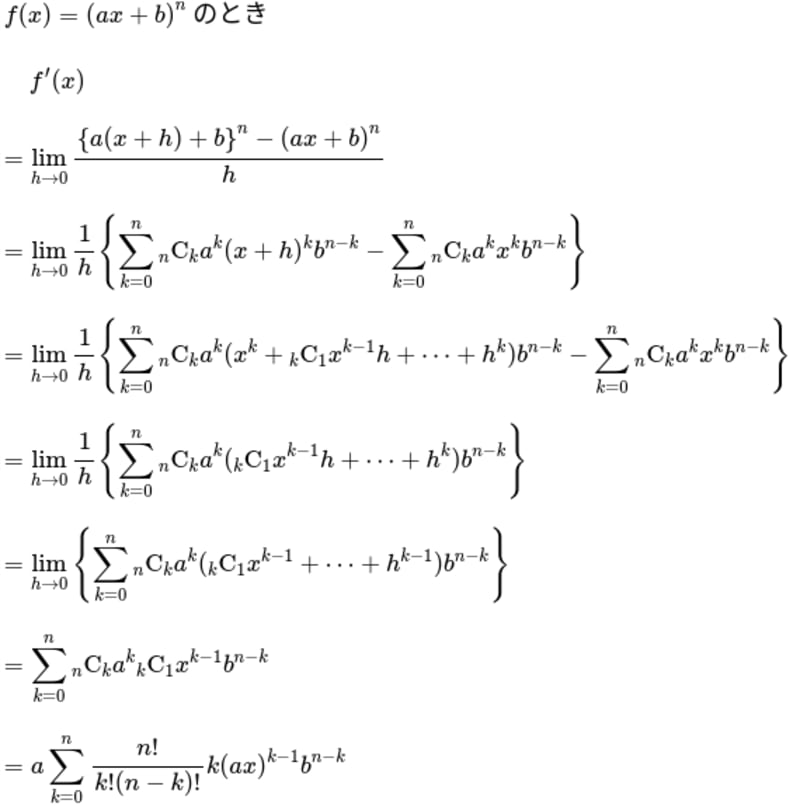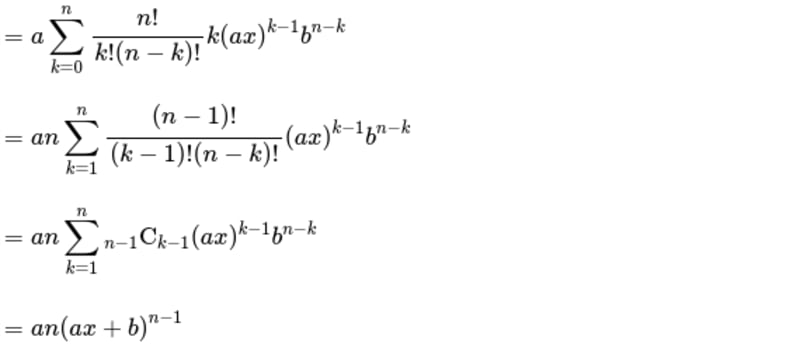数学の質問です。

つまり、$k=0$の時、$0$になるから、$k=1$からの場合だけを考えれば良いと言うことですか？

ですよね！１行目で和を求めている数列の $k=0$ の項は $0$ になりますからそれを除いても値は変わらないでしょう。それによって「$k$ を約分」できるようになってるということでしょう。

分かりました！

ありがとうございます！

因みに$0÷0$って定義されて居ないんでしたっけ？

少し気になるのは，$(ax+b)^n$ の導関数を求めているようにみえるのですが，それであれば，１行目から $k=0$ を除いておかないと，１行目が $x=0$ で定義されていないところです。

定数は微分すれば $0$ ですから，その時点で $k=1$ からにしておいた方がスッキリするかもしれません。

$0\div 0$ は定義されないことが多いです。

とくに，$0\div 0$ を

方程式 $0\times x=0$ の解

としてしまうと，

$0\div 0=0$

も

$0\div 0=1$

も成り立ってしまい，そこから

$0=1$

が導かれますが，これは $0\neq 1$ と矛盾します。

↑分かりました！

少し気になるのは，$(ax+b) ^n$の導関数を求めているようにみえるのですが，

→おっしゃる通り、この質問は他のサイトで、$(ax+b) ^n$の導関数の求め方を見て居た時に持った疑問です。

それであれば，$1$行目から$k=0$を除いておかないと，$1$行目が$x=0$で定義されていないところです。

→どう言う意味ですか？理解できなくて、、、

1行目の $(ax)^{k−1}$ の部分が $k=0$ のとき，$(ax)^{−1}$ となりますが，これは $x=0$ で定義されていないでしょう？

「$x=0$で定義される」とはどう言う意味ですか？

この写真が実際にそのサイトに載って居る証明ですが、この証明には穴がある？（間違って居る？）と言うことですか？

間違っているというほどのことはありませんが，$(ax)^{−1}=\displaystyle{ \frac{1}{ax} }$ で $x=0$ のとき，$\displaystyle{ \frac{1}{0} }$ となってしまいます。

また ${}_{0}\mathrm{C} _1$ を定義していないなら，下から８行目あたりから，$\displaystyle{ \sum_{k=1}^{n} }$ とした方が無難でしょう。

返信が遅くなってしまいすみません💦

また${}_0\mathrm{C}_1$を定義していないなら，下から８行目あたりから，$\sum_{k=1}^{n}$とした方が無難でしょう。

→読んで居て確かにそうだなーと思ったのですが、そもそも${}_0\mathrm{C}_1$は定義できるのですか？

定義することはあります。たいてい ${}_0\mathrm{C}_1$ に相当するものの値は $0$ とするようです。

そうなんですね！

色々ありがとうございました！

解決しました！

なによりです！