小学校4年生の問題ですが、答えが分かりません。教えてください。

結論から言うと、

・ア$+$イ$=24$

・ウやエはいくつであっても関係ない

だと言えるでしょう。

その理由を説明します。

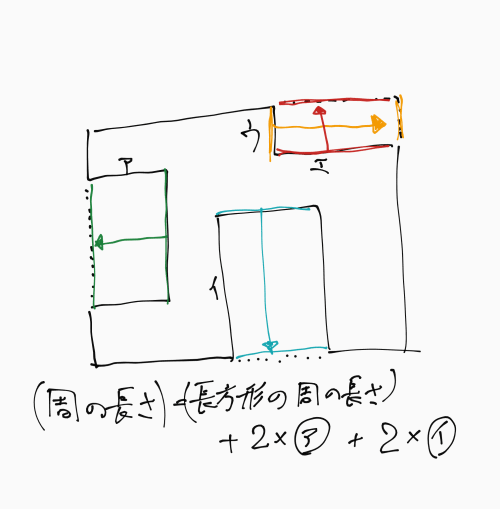
図１の点線部分に線を移動してみると、添付した図の紫色の線のようになります。

すると、周の長さ（周りの長さ）は、

長方形の周の長さ　$+$　$2×24$（$cm$）と表されます。

図２の点線部分に線を移動してみると、添付した図の緑、水色、赤、黄色の線のようになります。

すると、周の長さは、

長方形の周の長さ　$+$　$2×$ア　$+$　$2×$イと表されます。

よって、長方形の周の長さ　$+$　$2×24$（$cm$）$=$長方形の周の長さ　$+$　$2×$ア　$+$　$2×$イ

が成立します。

長方形の周の長さは左右一緒なので、両方からその分だけ引いても残りは同じになります。

だから、

$2×24$（$cm$）$=2×$ア　$+$　$2×$イ

が成立します。

等式の左右を両方半分にしても同じになるので、

$24$（$cm$）$=$ア$+$イ

となります。

つまり、この式を守ることが、図１・２を成立させる条件であるとも言えるでしょう。

この式にウやエは関わっていないので、ウやエはいくつであっても関係ない、と言えるでしょう。

長文失礼しました。またわからないことがあったら聞いてください！