, とし、不等式を考える。ただしは正の定数である。
(1) のとき、①はつねに成り立つことを示せ
(2)①がつねに成り立てば、であることを示せ。
(1)は模範解答のやり方が思いつかず遠回りしたのですが間違ってはないでしょうか?
(2)は模範解答がよくわかりません…。
なぜを調べるのですか?
また自分の解答はどうでしょうか?
いろいろ質問が多いですがその一部でも良いので教えていただけると嬉しいです!


ベストアンサー

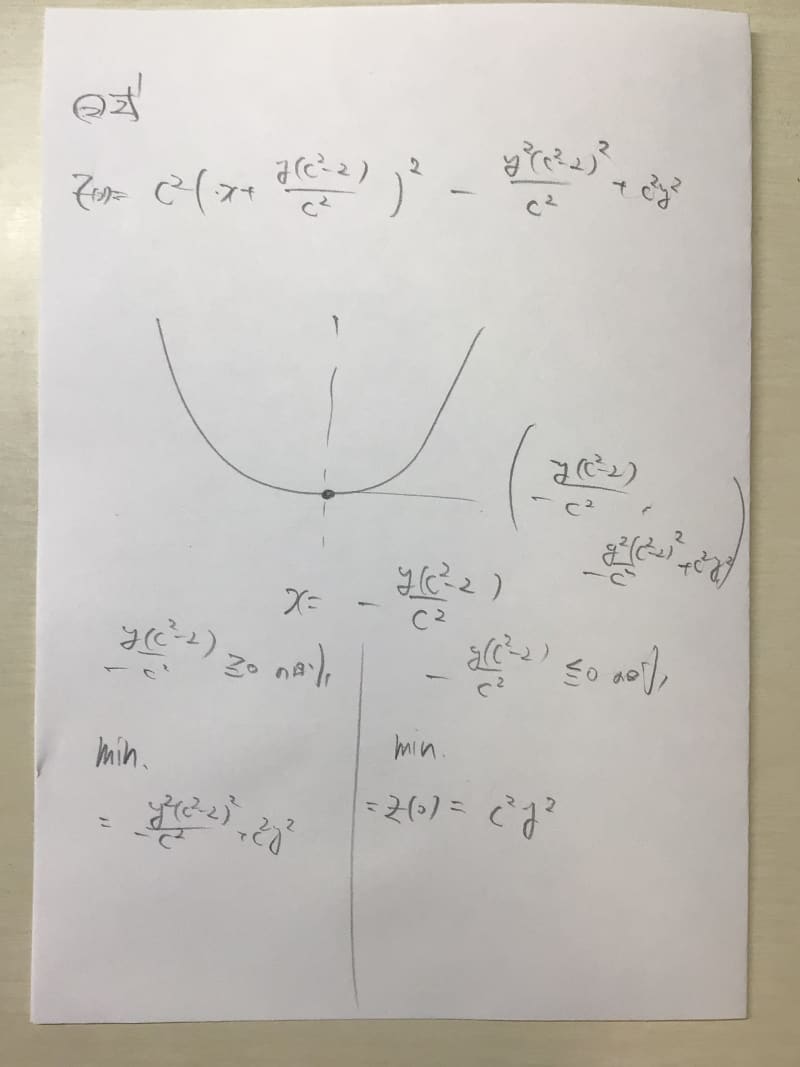
が正なのか負なのかはわからないので、最小値は、、、のところは場合分けが必要になります。
が の中に入っているのかどうかで最小値は変わります。
(2)でも同様です。場合分けをすれば合ってると思います。
なぜx=yとしたのかについて。
①式が常に成り立つ、というのは任意のx、y()に対して①式が成り立つということです。
だから頭の中でxとyに何を入れれば を導けるかな、と考えた時に
x=y=1ならいけるやんということでこういう解答になったのみです。
回答ありがとうございます!
(2)の模範解答わかりました!
は2乗しているのですが、それでも場合わけが必要ですか…?
正負によって最小値が変わるというのがよくわからないので、場合分けの仕方を詳しく教えていただけると嬉しいです!









質問者からのお礼コメント
返信もありがとうございます‼︎
場合分けの仕方もよくわかりました‼︎
そういう発想がなかったので、しっかり身につけていこうと思います‼︎
返信を見るのが遅くなってしまいすみません🙇