円の接線の方程式について
円が2つあって方程式はそれぞれC1:x^2+y^2=1,C2:(x-5)^2+y^2=4で、どっちにも接する接線の方程式を求めるのですが、
円との接点の座標を、小さい方の円→(a,b)、大きい方の円→(c,d)と置いて、
接線の方程式の公式使って係数比較でやってみたんですが、接点のy座標が同じというあり得ない答えになります。(画像参照)何が間違ってるのでしょうか?
ちなみに正解は画像二枚目のような方程式です。

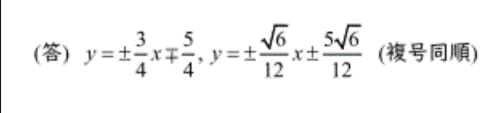
ベストアンサー

同じ直線を表す2つの方程式の係数が一致するというのは誤りで、正しくは「係数比」が一致するです。
簡単な例で言うと、
の2つの直線は、係数は異なりますが同じ直線を表していますね。こういうことです。
今回だと、直線 と、直線 が一致するので、
が立式でき、これを満たす実数の組 を探せばよいということになります。
ちなみに余談ですが、円の接線が出てくる問題では、まずは「中心と接線の距離が半径と等しい」を使うことを考えましょう。
今回では、円 の接線は、その接点の座標を とすると となり、この直線と円 の中心 との距離を考えて、
とするとこの直線は円 にも接する。
これで計算量は大幅に減らせます。
回答有り難うございます。他の回答者の方も、ありがとうございます。
係数比較は比が同じというだけでイコールではないということがわかりましたが、
複素数のときは例えば
a+bi=c+diの時に、a=c,b=d
とやると思うのですが、これはなんでオッケイなのでしょうか?
それは の形で表されている複素数は、 の形以外に表しようがないからです。
今回の問題は方程式ですから、同じものを表していても異なる表記の仕方があります。
数はただ一通りにしか表せないが、式には何通りもの表し方があるということです。








