(2)でどこが間違ってますか？

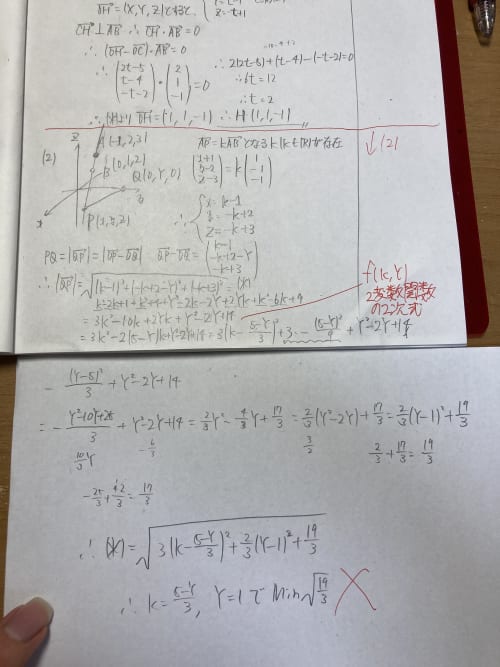
(*)の計算ミスですね。

$$\begin{align*}|\overrightarrow{PQ}|^2&=\sqrt{(k-1)^2+(-k+2-Y)^2+(-k+3)^2}\\&=\sqrt{F(k,Y)}\end{align*}$$

とすれば、

$$\begin{align*}F(k,Y)&=(k-1)^2+(-k+2-Y)^2+(-k+3)^2\\&=(k^2-2k+1)+\{k^2-2k(2-Y)+(2-Y)^2\}+(k^2-6k+9)\\&=3k^2-2k\{1+(2-Y)+3\}+\{1+(2-Y)^2+9\}\\&=3k^2-2k(6-Y)+\{(2-Y)^2+10\}\\&=3\left(k-\dfrac{6-Y}{3}\right)^2-3\left(\dfrac{6-Y}{3}\right)^2+\{(2-Y)^2+10\}\\&=3\left(k-\dfrac{6-Y}{3}\right)^2-\left\{\dfrac{36-12Y+Y^2}{3}-(4-4Y+Y^2)-10\right\}\\&=3\left(k-\dfrac{6-Y}{3}\right)^2-\dfrac{(36-12Y+Y^2)-3(4-4Y+Y^2)-30}{3}\\&=3\left(k-\dfrac{6-Y}{3}\right)^2-\dfrac{-2Y^2-6}{3}\\&=3\left(k-\dfrac{6-Y}{3}\right)^2+\dfrac{2}{3}Y^2+2\\\end{align*}$$

$F(k,Y)$は$k=\dfrac{6-Y}{3}$で最小値$\dfrac{2}{3}Y^2+2$をとる。

$\dfrac{2}{3}Y^2+2$は$Y=0$で最小値$2$をとる。

よって$F(k,Y)$は$Y=0,k=2$で最小値$2$をとる。