問題
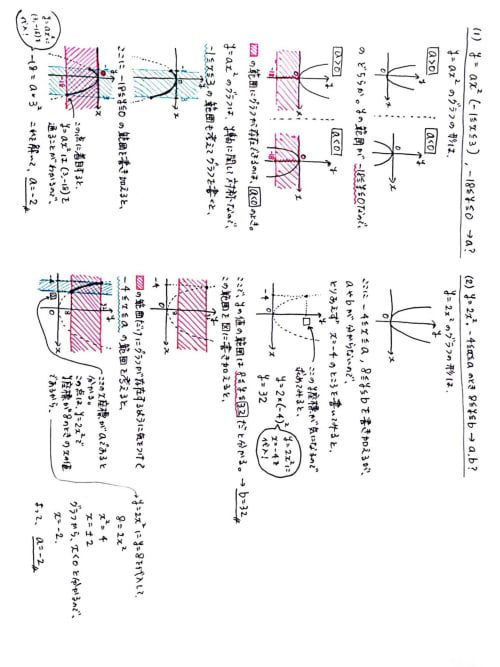
(1) 関数y=ax²(-1≦x≦3)のyの変域-18≦y≦0である。aの値を求めよ。
(2) 関数y=2x²は、-4≦x≦aのとき8≦y≦bである。a,bの値を求めよ。
よろしくお願いします。 中学3年の知識でバカでも分かるように教えてください。
ベストアンサー

(1)
y=ax²(-1≦x≦3)のyの範囲が-18以上と負の値を取っているからa<0であることがわかります。
関数に範囲のx=-1,x=3を代入してみると
それぞれy=aとy=9aであることがわかります。
実際にグラフを書いてみるとa<0より、
y=9aの方がy=aよりも小さいことが分かる。_①
またy=ax²はa<0のときy=0が最大になる。_②
①②より9a≦y≦0と表せます。
yの変域が-18≦y≦0であることを考慮すると9a=-18 a=-2 になります。
よって(1)の答えはa=-2
(2)
(1)と同じように考えてみましょう。
まずy=2x²のグラフを書いてみると
値は必ず0以上(0≦y)と分かる。③
x=-4,x=aをy=2x²にそれぞれ代入すると
y=32 y=2a²と表せます。④
ここでaが正の数か負の数かで③④から求められるyの変域が変わります。
[aが正の値のとき] 結論:誤り
関数y=2x²は最小値のy=0をとるから
0≦y≦〜(〜は32,2a²のどちらか)と表せます。でも問題の 8≦y≦b と比べると
0と8で違うのでダメですね。
[aが負の値のとき]
関数はx=-4のとき最大値y=32,x=aのとき最小値y=2a²であるとわかります。
{もし分からなかったらとにかくグラフを書いてどっちが高いか比べましょう}
よってyの変域は 2a²≦y≦32 、
これを問題より 8≦y≦bと比べて
2a²=8 これをといてa=-2(aは負の値!)
b=32
(2)答えはa=-2, b=32
まとめ
グラフを大雑把で良いから書く
yの変域を文字を使って自分で作る
問題で与えられたyの変域と比べる