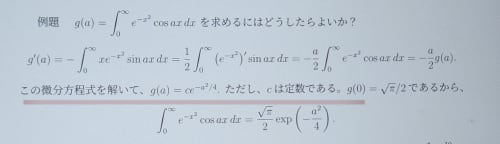写真の問題について質問なのですが、

①微分方程式$$g'(a)=-\dfrac{a}{2}g(a)$$

分かりやすくするために、$y=g(a)$ とおきます。$g'(a)=\dfrac{dy}{da}$ なので、微分方程式は次のようになります。

$$\dfrac{dy}{da}=-\dfrac{a}{2}y \iff \dfrac{dy}{y}=-\dfrac{a}{2}da$$

この両辺を積分して、

$$\log|y|=-\dfrac{a^2}{4}+c_0$$

となります。ただし $c$ は任意定数です。したがって、

$$\begin{aligned}y&=\pm e^{-\frac{a^2}{4}+c_0}\\&=ce^{-\frac{a^2}{4}}\end{aligned}$$

となります。$c=\pm e^{c_0}$ となる新たな任意定数 $c$ に置き換えています。

これで微分方程式の一般解が求められました。任意定数 $c$ は何でもよい定数です。一階微分方程式の一般解には必ず任意定数が $1$ つ含まれます。原始関数が一意に定まらないのと同じことです。

②先ほどの任意定数の値を定めるためには、ある $a$ での $g(a)$ を考えなければならず、だいたいは初期条件として $g(0)$ の値を考えることが多いです($c=g(0)$ であって式の形が簡単になるため)。

$$g(0)=\int_0^\infty e^{-x^2}dx \quad (=I \text{ とおく})$$

となるので、この値を求めます。ガウス積分と呼ばれる有名な広義積分です。

$$I=\int_0^\infty e^{-x^2}dx=\int_0^\infty e^{-y^2}dy$$

なので、

$$\begin{aligned}I^2&=\left(\int_0^\infty e^{-x^2}dx\right)\left(\int_0^\infty e^{-y^2}dy\right) \\&=\int_0^\infty \int_0^\infty e^{-(x^2+y^2)} dxdy\end{aligned}$$

となります。

ここで、$x=r\cos\theta,y=r\sin\theta$ という極座標変換により、$$x^2+y^2=r^2,\ dxdy=rdrd\theta$$であり、$\begin{array}{c|c} x,y & 0 \to \infty\end{array}$ において $\begin{array}{c|c}r & 0\to\infty \end{array},\begin{array}{c|c}\theta & 0\to\frac{\pi}{2} \end{array}$ となるので、

$$\begin{aligned}I^2&=\int_0^\infty \int_0^\infty e^{-(x^2+y^2)} dxdy \\&=\int_0^{\frac{\pi}{2}} \int_0^\infty e^{-r^2} rdrd\theta \\&=\int_0^{\frac{\pi}{2}} \left[-\dfrac{e^{-r^2}}{2}\right]_0^\infty d\theta \\&=\int_0^{\frac{\pi}{2}} \dfrac{\pi}{2} d\theta \\&=\dfrac{\pi}{4}\end{aligned}$$

となり、$I=\dfrac{\sqrt{\pi}}{2}$ が得られます。