中学受験算数です。

(1)

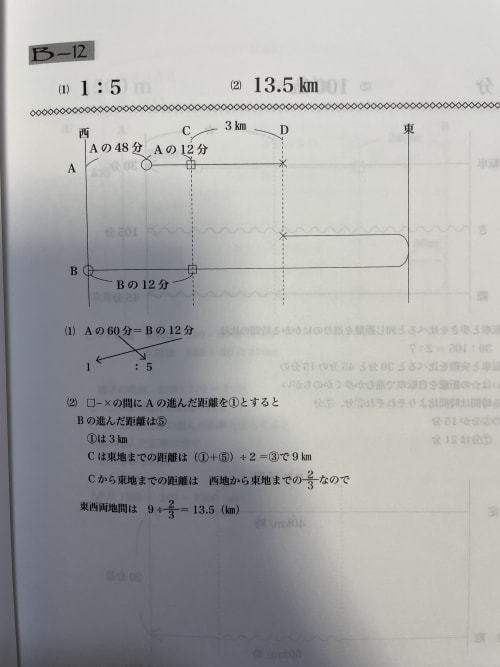
西地～C地点までにかかった時間は

　A君：60分

　B君：60-48＝12分

なので、二人の速さはそれぞれ

　A君：(西地～C地点の距離)$\div$60分

　B君：(西地～C地点の距離)$\div$12分

で求めることが出来ます。

よって二人の速さの比は

$$\begin{align*}&\phantom{=}\text{A君の速さ:B君の速さ}\\&=\text{(西地～C地点の距離)}\div\text{60分}:\text{(西地～C地点の距離)}\div\text{12分}\\&=\dfrac{1}{60}:\dfrac{1}{12}\\&=1:5\end{align*}$$

となります。

(2)

A君が進んだC地点～D地点は$3\mathrm{km}$です。

(1)で速さの比が1:5だと分かっているので、同じ時間でB君はA君の5倍である$15\mathrm{km}$を進んだことになります。

このとき、二人の進んだ区間を調べると次のようになります。

　A君：C地点～D地点＝3km

　B君：C地点～東地+東地～D地点＝15km

ここで、二人の進んだ距離を足してみると

$$\begin{align*}　&\phantom{=}\text{C地点～D地点}+\text{(C地点～東地}+\text{東地～D地点)}\\&=\text{C地点～D地点}+\text{(C地点～東地}+\text{D地点～東地)}\\&=\text{(C地点～D地点}+\text{D地点～東地)}+\text{C地点～東地}\\&=\text{C地点～東地}+\text{C地点～東地}\\&=2\times\text{(C地点～東地)}\end{align*}$$

となるので、C地点～東地の距離はA君とB君が進んだ距離を足して2で割ると求めることが出来ます。

よって

$$\text{(C地点～東地)}=(3+15)\div2=9\mathrm{km}$$

C地点は西地～東地の$\dfrac{1}{3}$の地点であったので、C地点～東地の距離は西地～東地の$\dfrac{2}{3}$であることが分かります。

よって、求める西地～東地の距離は

$$9\div\dfrac{2}{3}=13.5\mathrm{km}$$

となります。