GMARCHの一つの大学附則高校の受験問題について質問です。解き方を教えてください

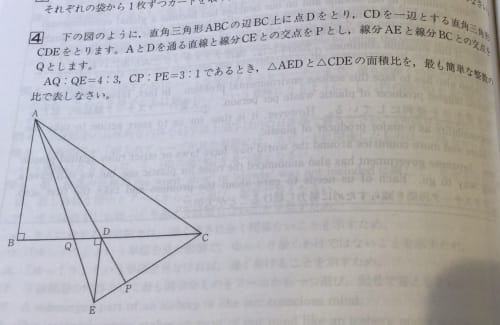
$\triangle AED$と$\triangle CDE$の面積比は共通の辺$DE$を底辺とすれば高さの比、すなわち$BD:CD$(★)で表せる。

点$Q$を通り、線分$AP$に平行な直線と線分$CE$との交点を点$R$とすると

$\triangle CDP\varpropto\triangle CQR$より

$$CD:DQ=CP:PR$$

$\triangle ERQ\varpropto\triangle EPA$より

$$ER:RP=EQ:QA=3:4$$

また、問題から

$$CP:PE=3:1$$

よって、$ER=3x$とおくと$RP=4x$となり、$CP=3EP=21x$であるから、

$$CD:DQ=CP:PR=21x:4x=21:4$$

となるので、$CD=21y$とおけば$DQ=4y$である。

さらに、$BQ:QD=AQ:QC=4:3$より

$$BQ=\dfrac{4}{3}QD=\dfrac{16y}{3}$$

であるから、求める面積比は(★)より

$$\begin{align*}BD:CD&=(BQ+QD):CD\\&=\left(\dfrac{16y}{3}+4y\right):21y\\&=\dfrac{28y}{3}:21y\\&=4:9\end{align*}$$

である。$\square$

--------------------------

別解

メネラウスの定理から

$$\dfrac{CP}{PE}\cdot\dfrac{EA}{AQ}\cdot\dfrac{QD}{DC}=1$$

これに$AQ:QE=4:3,CP:PE=3:1$を代入して

$$\begin{align*}\dfrac{3}{1}\cdot\dfrac{7}{4}\cdot\dfrac{QD}{DC}&=1\\\dfrac{QD}{DC}&=\dfrac{4}{21}\\QD:DC&=4:21\end{align*}$$

よって$\triangle AED$と$\triangle CDE$の面積比は

$$\begin{align*}BD:DC&=(BQ+QD):DC\\&=\left(\dfrac{4}{3}QD+QD\right):\dfrac{21}{4}QD\\&=\dfrac{7}{3}:\dfrac{21}{4}\\&=4:9\end{align*}$$

である。$\square$