まず a について整理していきましょう。
(a+b)(b+c)(c+a)+abc=(b+c)(a+b)(a+c)+bca=(b+c){a2+(b+c)a+bc}+bca=(b+c)a2+(b+c)2a+bc(b+c)+bca=(b+c)a2+(b2+3bc+c2)a+bc(b+c)
a の係数に着目してたすき掛けをします。
a の二次方程式と考えてください。
ここからは画像も見てください。
(b+c)(b+c)+1⋅bc=b2+3bc+c2
であることに注目すると
(b+c)a2+(b2+3bc+c2)a+bc(b+c)={a+(b+c)}{(b+c)a+bc}=(a+b+c)(ab+bc+ca)
となります。
以上から
(a+b)(b+c)(c+a)+abc=(a+b+c)(ab+bc+ca)
と因数分解できることがわかります。

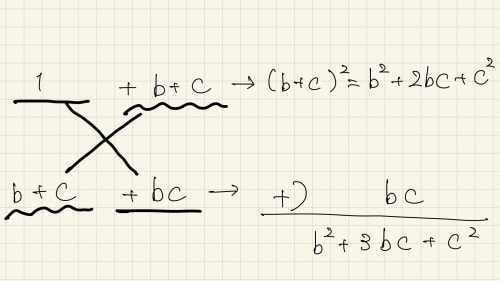

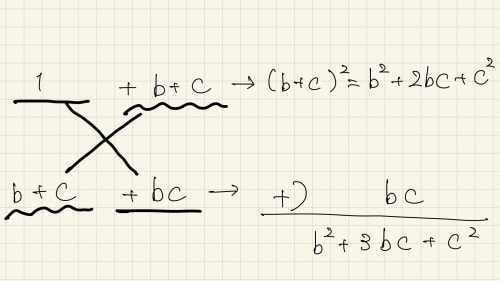
質問者からのお礼コメント
よくわかりました。ありがとうございます。