解決済み
dxをeにかけると思うんですが、なぜこうならないのでしょうか
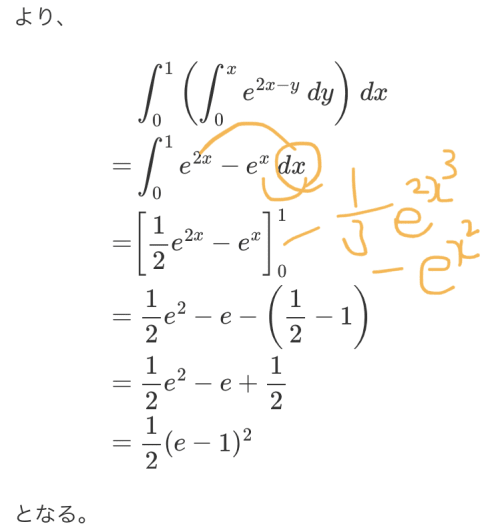
ベストアンサー

,
,
,
です。
オレンジ文字から推察するに、
だと思われているようですがこれは誤りです。
と置いて計算してみると
となり、 とは一致しません。
シェアしよう!
そのほかの回答(1件)
削除済みユーザー
2021/6/23 23:23
Dxっていうのはかけるものではない
かくものだ
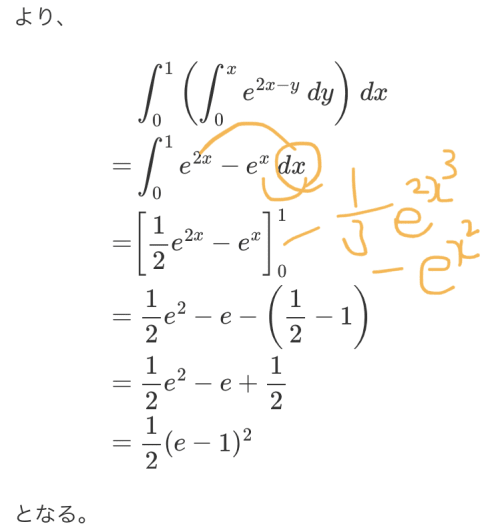

,
,
です。
オレンジ文字から推察するに、
だと思われているようですがこれは誤りです。
と置いて計算してみると
となり、 とは一致しません。
削除済みユーザー
かくものだ