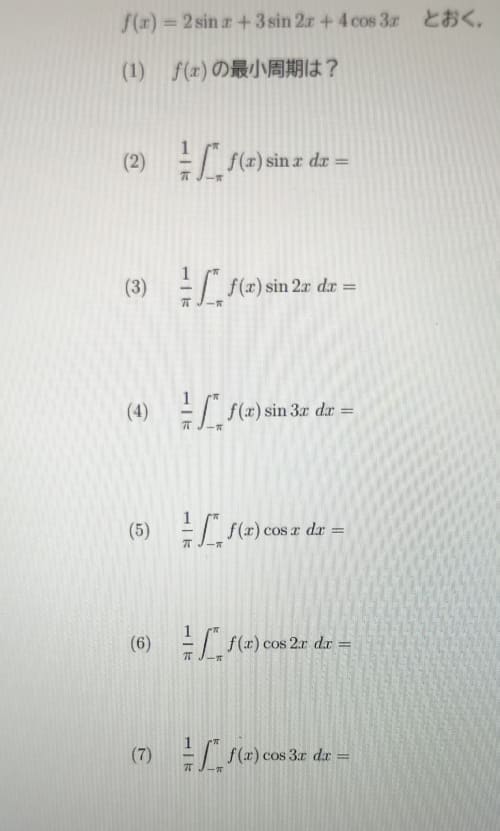全部わかんないのですが全部は大変なので(1)、(2)、(3)の問題の解説をお願いします

偶関数と奇関数を見つけてうまく積分しましょう。

積分範囲が $- \pi \to \pi$ なので、積分計算をするまでもなく奇関数の積分が0になるからです。

偶関数と奇関数がわからない場合はこれを読んだらわかります。

→https://manabitimes.jp/math/1052

まず、$f(x)$ は

$$\begin{aligned}f(x) &= 2 \sin x + 3 \sin 2x + 4 \cos 3x \\ &= \text{（奇関数）+（奇関数）+（偶関数） }\end{aligned}$$

（1）$2 \pi$

（2）

$$\begin{aligned}f(x) \sin x &= (2 \sin x + 3 \sin 2x + 4 \cos 3x) \sin x \\ &= \text{ [(奇関数)+(奇関数)+(偶関数)] } \times \text{ (奇関数) } \\ &= \text{ [(偶関数)+(偶関数)+(奇関数)] }\end{aligned}$$

つまり、前の2つの項は偶関数で、最後の項は奇関数になります。

$$\begin{aligned}& \int_{- \pi}^{\pi} f(x) \sin x \, dx \\&= \int_{- \pi}^{\pi} \text{ [(偶関数)+(偶関数)+(奇関数)] } \, dx \\&= 2 \int_{0}^{\pi} \text{ [(偶関数)+(偶関数)] } \, dx \\&= 2 \int_{0}^{\pi} ( 2 \sin^2 x + 3 \sin 2x \sin x ) \, dx \\&= 2 \int_{0}^{\pi} ( (1 - \cos 2x) + 6 \sin^2 x \cos x ) \, dx \\&= 2 [x - \dfrac{1}{2} \sin 2x + 2 \sin^3 x]_{0}^{\pi} \\&= 2 \pi\end{aligned}$$

よって、

$$\dfrac{1}{\pi} \int_{- \pi}^{\pi} f(x) \sin x \, dx = 2$$

です。

（3）

同様に、

$$\begin{aligned}& \int_{- \pi}^{\pi} f(x) \sin 2x \, dx \\&= \int_{- \pi}^{\pi} \text{ [(偶関数)+(偶関数)+(奇関数)] } \, dx \\&= 2 \int_{0}^{\pi} \text{ [(偶関数)+(偶関数)] } \, dx \\&= 2 \int_{0}^{\pi} ( 2 \sin x \sin 2x + 3 \sin^2 2x) \, dx\end{aligned}$$

(2)の過程で答えが分かっている積分結果を有効活用しましょう。

$$\begin{aligned}& \int_{- \pi}^{\pi} f(x) \sin 2x \, dx \\&= 6 \int_{0}^{\pi} \sin^2 2x \, dx \\&= 6 \cdot \dfrac{\pi}{2} \\&= 3 \pi \\& \therefore \dfrac{1}{\pi} \int_{- \pi}^{\pi} f(x) \sin 2x \, dx = 3\end{aligned}$$

（4）

$$\dfrac{1}{\pi} \int_{- \pi}^{\pi} f(x) \sin 3x \, dx = 0$$