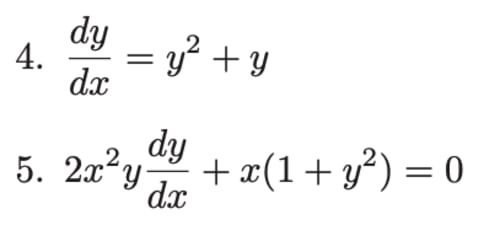画像の微分方程式の問題の解き方がわかりません！

友達がおっしゃるように、変数分離形の微分方程式ですね！

変数分離形の微分方程式は、解き方がパターン化されているので、暗記するイメージでとにかく問題をこなすのが個人的にはおすすめです！

（4）

$$\dfrac{dy}{dx} = y^2 + y$$

両辺を $y^2 + y$ で割りましょう。ただし、$y \neq 0, -1$ です。

$$\begin{aligned}\dfrac{1}{y^2 + y} \dfrac{dy}{dx} &= 1 \\\dfrac{1}{y(y + 1)} \dfrac{dy}{dx} &= 1 \\(\dfrac{1}{y} - \dfrac{1}{y+1}) dy &= dx \\\end{aligned}$$

両辺を積分します。（不定積分）

$$\begin{aligned}\int (\dfrac{1}{y} - \dfrac{1}{y+1}) dy &= \int dx \\\log |y| - \log |y + 1| &= x + C \\\log |\dfrac{y}{y+1}| &= x + C \\|\dfrac{y}{y+1}| &= e^{x + C} \\\dfrac{y}{y+1} &= A e^x \\\end{aligned}$$

最後のところで $A = \pm e^C$ としてます。この辺も大胆にやっちゃってOKです。

$$\begin{aligned}\dfrac{y}{y+1} &= A e^x \\\iff y &= \dfrac{A e^x}{1 - A e^x}\end{aligned}$$

また、$y = 0, -1$ も解です。

$y = 0$ は $A = 0$ にまとめられます。

（答）$y = \dfrac{A e^x}{1 - A e^x}, \quad y = -1$

（５）

両辺を $x(1 + y^2)$ で割ればOKです！

$$\int \dfrac{2y}{y^2 + 1} dy = - \int \dfrac{1}{x} dx$$

となります。（４）と同様に計算します。後は答えだけ書いておきますね。

（答）$y^2 = \dfrac{A}{x} - 1$