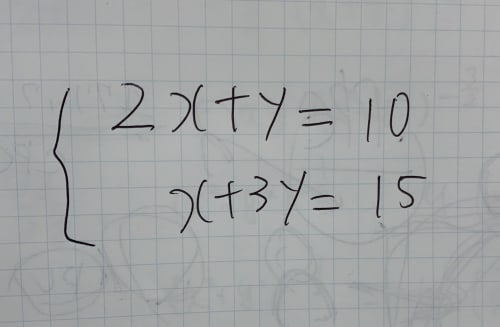連立方程式の計算方法を教えてください。どうやったらxとyが出せますか？

連立方程式を解く時は次の手順で考えましょう！✊

1. 式に①②と番号を書く。

2. x と y のどちらを先に求めるかを決める。

3. 求めない方の文字を消す。（加減法・代入法）

4. 先に求める方の値を求める。

5. もう片方の値も求める。

それでは順番にやっていきましょう！

1. 式に①②と番号を書く

$$\begin{cases}2x + y = 10 \quad \cdots \text{①}\\x + 3y = 15 \quad \cdots \text{②}\end{cases}$$

2. x と y のどちらを先に求めるかを決める

どちらを先に求めてもOKです！どちらからでもできます。

求めやすいと思った方を先に求めるといいですよ。

うまくいかなかったら別の方から始めるようにしましょう！

今回は $x$ を先に求めましょう！

なので、先に $y$ を消去しましょう。

3. 求めない方の文字を消す　＆　4. 先に求める方の値を求める。

$y$ を消しましょう！

【加減法の場合】

$$\begin{cases}2x + y = 10 \quad \cdots \text{①}\\x + 3y = 15 \quad \cdots \text{②}\end{cases}$$

$y$ の係数を揃えます。そのために①の式の両辺を3倍しましょう！

$$\begin{cases}6x + 3y = 30 \quad \cdots \text{①} \times 3 \\x + 3y = 15 \quad \cdots \text{②}\end{cases}$$

（上の式）ー （下の式）をしましょう。

$5x = 15$ よって、 $x = 3$ です。

【代入法の場合】

$$\begin{cases}2x + y = 10 \quad \cdots \text{①}\\x + 3y = 15 \quad \cdots \text{②}\end{cases}$$

①より、 $y = 10 - 2x$

②に代入すると

$$\begin{aligned}x + 3(10 - 2x) &= 15 \\-5x + 30 &= 15 \\-5x &= -15 \\5x &= 15 \\x &= 3\end{aligned}$$

加減法でも代入法でも、答えは同じですよ！

5. もう片方の値も求める。

ここまでで、 $x = 3$ がわかりました。

連立方程式は、$x, y$ をセットで解答する必要があります。

$2x + y = 10$ と $x = 3$ より、

$$\begin{aligned}y &= 10 - 2x \\&= 10 - 2 \times 3 \\&= 4\end{aligned}$$

答えは

$$\begin{cases}x = 3 \\y = 4\end{cases}$$

です！

答えが出たら、問題文

$$\begin{cases}2x + y = 10 \quad \cdots \text{①}\\x + 3y = 15 \quad \cdots \text{②}\end{cases}$$

の式に、$x$ と $y$ を代入して成り立つかどうかを確認しましょう！

これで計算ミスもきっとなくなるはずです😄