z=x2+y2y=y(x2+y2)−21
そこで、
f(y)=y,g(x,y)=(x2+y2)−21
と置いてみましょう。つまり z=f(y)g(x,y) です。
下準備をしてみましょう。
まず f(y) について
∂x∂f(y)=0,∂y∂f(y)=1,
次に g(x,y) について
∂x∂g(x,y)∂y∂g(x,y)=∂x∂(x2+y2)−21=−21(x2+y2)−23⋅(2x)=−x(x2+y2)−23,=−y(x2+y2)−23,
ここまではただの偏微分です。まずは x で偏微分。
∂x∂z=∂x∂(f(y)g(x,y))=f(y)∂x∂g(x,y)=y⋅(−x)(x2+y2)−23=−xy(x2+y2)−23
y でも同様です。
∂y∂z=∂y∂(f(y)g(x,y))=∂y∂f(y)g(x,y)+f(y)∂y∂g(x,y)=1⋅(x2+y2)−21+y⋅[−y(x2+y2)−23]=(x2+y2)−23[(x2+y2)−y2]=x2(x2+y2)−23
丁寧にひとつずつ偏微分すれば大丈夫ですよ!頑張ってください

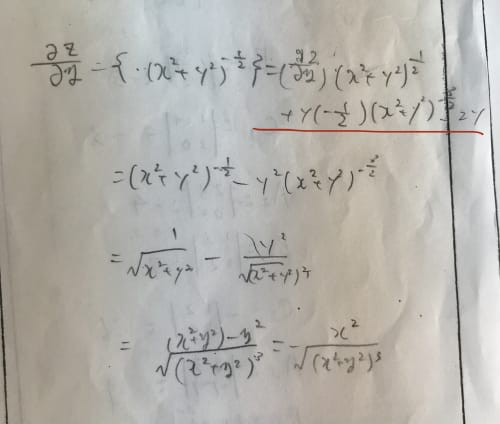


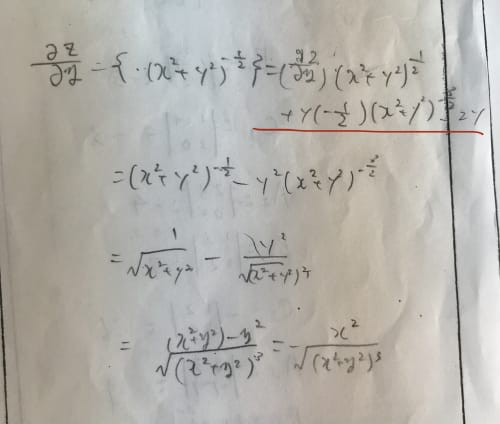

質問者からのお礼コメント
ありがとうございます!