この前の質問は，不十分でしたので，言い直して質問です。

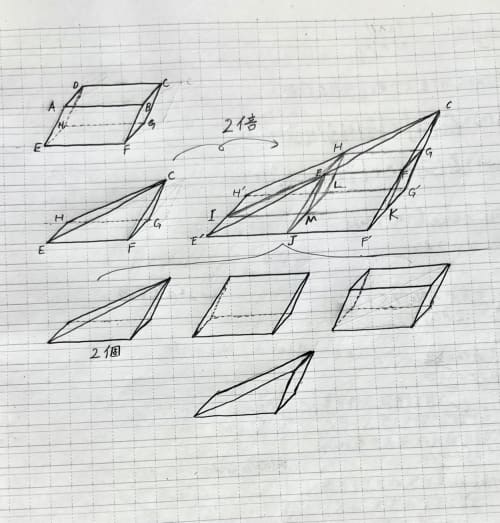
図のような平行六面体$ABCD-EFGH$と、その部分集合である四角錐$C-EFGH$を考える。

立体$K$の体積を$V(K)$と表すことにする。

ここで、以下の命題を認める

①相似比が$1:a$となる2つの立体の体積比は$1:a^3$となる

②ある立体$K$が切断により$K_1$と$K_2$に分かれるとき、$V(K)=V(K_1)+V(K_2)$

(証明は面倒なのでここではしません。錐体の体積の公式は使わずに証明できます)

四角錐$C-EFGH$との相似比が$1:2$となるような四角錐$C-E'F'G'H'$を考える。さらに、図のように5点$I,J,K,L,M$を新たにおく

$V(C-EFGH)=v,V(ABCD-EFGH)=V$とおく

②より

$V(C-E'F'G'H')$

$=V(C-EFGH)+V(E-E'JMI)+V(EIM-HH'L)+V(EJM-FF'K)+V(EFGH-MKG'L)$

となる

①より

$V(C-EFGH):V(C-E'F'G'H')=1:8$

よって$V(C-E'F'G'H')=8v$

四角錐$E-E'JMI$は四角錐$C-EFGH$と合同である

①より

$V(C-EFGH):V(E-E'JMI)=1:1$

よって$V(E-E'JMI)=v$

立体$EIM-HH'L$および立体$EJM-FF'K$は反転合同なもう一つの立体と組み合わせることにより平行六面体$ABCD-EFGH$と合同となるため、①②より

$2V(EIM-HH'L)=2V(EJM-FF'K)=V$

よって$\displaystyle V(EIM-HH'L)=V(EJM-FF'K)=\frac{1}{2}V$

平行六面体$EFGH-MKG'L$は平行六面体$ABCD-EFGH$と合同であるため、①より

$V(EFGH-MKG'L)=V$

したがって、$\displaystyle 8v=v+v+\frac{1}{2}V+\frac{1}{2}V+V$

$\displaystyle v=\frac{1}{3}V$

かなり面倒ですが、このようにして積分や錐体の体積の公式を使わずに、斜錐体の体積の公式を証明することは可能です