任意の a に対して f(x)=1+a2−2acosxsin2x が区間 [0,π] 上連続であることは確認済みとします。
∣a∣=1 と仮定します。計算量が多めにはなりますが(他のうまい方法が思いつけなかったので)定石どおり,
t=tan2x,sinx=1+t22t,cosx=1+t21−t2
とおいて,f(x) を t の有理式に直します。
∫f(x)dx=∫1+a2−2a1+t21−t2(1+t22t)2dtdxdt=8∫((1+a)2t2+(1−a)2)(t2+1)2t2dt
簡単のために P=1+a,Q=1−a とおきます。A,B,C を t に関わらない定数とし,部分分数に分解して,有理関数の不定積分の公式(https://mecs.jp/SHIBAURA/calcwrec1/lecture8.pdf)を適用すると,
∫f(x)dx=8∫(Pt2+Q2)(t2+1)2t2dt=8∫{Pt2+Q2A+t2+1B+(t2+1)2C}dt=8{PQAtan−1(QPt)+Btan−1t+2C(tan−1t+t2+1t)}+C′
これで不定積分が求まりました。
定積分を求めます。x が積分区間 (0,π) を動くとき t=tan(x/2) は区間 (0,+∞) を動くので,
∫0πf(x)dx=8x→+∞lim[PQAtan−1(QPt)+Btan−1t+2C(tan−1t+t2+1t)]0x
tan−1t→π/2,t/(t2+1)→0 となること,また tan−1(P/Q)t については P/Q<0 ならば →−π/2,P/Q>0 ならば →π/2 となることに注意して,
∫0πf(x)dx=4π[PQAsgn(QP)+B+2C]
ここで定数 A,B,C を具体的に求めてみると
ABC=(P2−Q2)2−P2Q2=16a2−(1−a2)2,=(P2−Q2)2Q2=16a2(1−a)2,=P2−Q21=4a1
よって簡単な計算から,
∫0πf(x)dx={π/(2a2)π/2(P/Q<0)(P/Q>0)
ここで P/Q<0⟺∣a∣>1,P/Q>0⟺∣a∣<1 であることを考えると目的の結果がしたがいます。
∣a∣=1 の場合については,{fa(x)} の一様収束性から
I(a)=∫0πfa(x)dx
は a=±1 で連続であり,上で得た結果から I(±1)=π/2 がしたがいます。
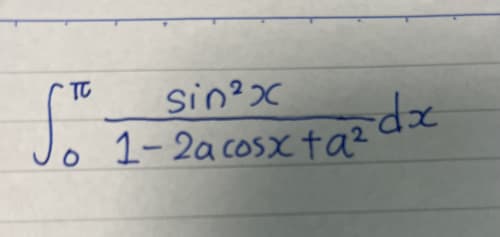





質問者からのお礼コメント
有理関数の積分についてのリンクまで載せてくださりありがとうございます!!
解答がとても分かり易くて感動しました!!!
有理関数の部分分数分解についての理解が浅く、P=1+a, Q=1-a と置くという発想が全くなかったのでkagomekagomeさんに答えていただけて本当に助かりました。
正直、この問題でこんなに早く解答が来ると思っていなかったのですごく驚いてます。
本当にありがとうございました!🙏🙏🙏👏