数学Iの正弦定理、余弦定理の問題です。(2)と(3)の求め方と答えを教えて頂きたいです。

(2)

(1) の [3] に書いてあるように、$a$ の $2$ 次方程式を立てることにします。そのためには

$$c^2 = a^2 + b^2 - 2ab\cos C$$

に現われている $a$ 以外の値をすべて求めておかなければなりません。いまの場合、$b, c, \cos C$ の $3$ つです。$c$ については問題文で与えられているとおり $c = \sqrt{6}$。また $\cos C$ については $C = 60^\circ$ なので $\cos C = \dfrac{1}{2}$ が分かっています。

　$b$ については、[2] に書いてあるとおり正弦定理で求まります。実際、正弦定理によれば、

$$\frac{b}{\sin B} = \frac{c}{\sin C}$$

ですから

$$\frac{b}{\sqrt{2}/2} = \frac{\sqrt{6}}{\sqrt{3}/2}$$

という $1$ 次方程式が立ちます。これを解けば $b = 2$ が求まります。

　さて、こうして求めた $b, c, \cos C$ の値を $c^2 = a^2 + b^2 - 2ab\cos C$ へ代入します。

$$\sqrt{6}^2 = a^2 + 2^2 - 2a \cdot 2 \cdot \frac{1}{2}$$

これを整理すれば、

$$a^2 - 2a -2 = 0$$

という $2$ 次方程式が立ちます。すると、$2$ 次方程式の解の公式から

$$a = \frac{2 \pm \sqrt{12}}{2} = 1 \pm \sqrt{3}$$

が求まります。ところが、この $2$ つの解のうち $1 - \sqrt{3}$ の方は負の数です（$1 < \sqrt{3} = 1.732\cdots$）ので、辺の長さとしてふさわしくありません。よって

$$a = 1 + \sqrt{3}$$

が答えとなります。

(3)

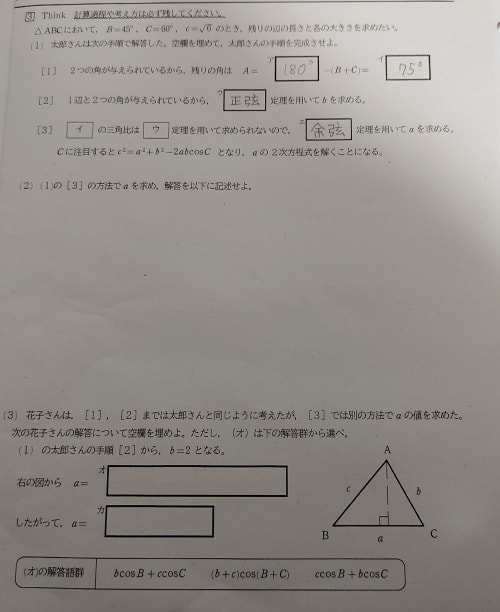
点 $A$ から辺 $BC$ へ下ろした垂線の足を $H$ とします。$\cos$ の定義により、$BH = c\cos B$； $CH = b\cos C$ です。よって $a = BH + CH = c\cos B + b\cos C$ です。

　あとはこの式へ $b, c, \cos B, \cos C$ の値を代入すれば、

$$a = \sqrt{6}\cdot\frac{\sqrt{2}}{2} + 2\cdot\frac{1}{2} = \sqrt{3} + 1$$

が求まります。