画像分かりにくくてすみません、中学受験用の問題を小学生に説明したいので答えの求め方をお願いします。

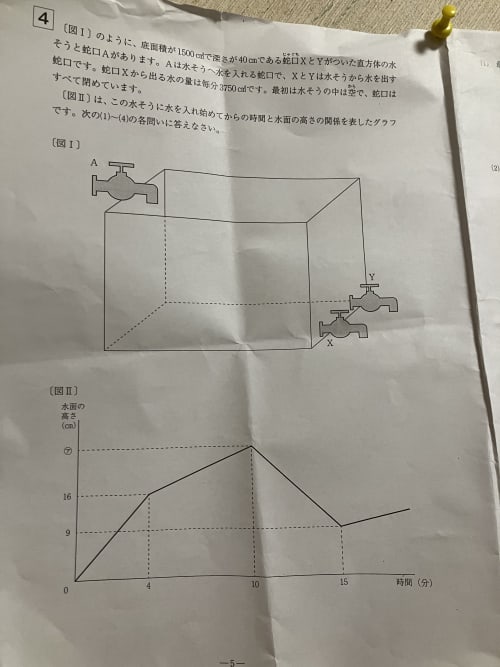
(1)グラフから、4分のとき高さ16$\mathrm{cm}$まで水が入る。

$$16\div4=4$$

よって毎分4$\mathrm{cm}$ずつ貯まることが分かる。また、水槽の底面積は1500$\mathrm{cm^2}$なので、Aから入る水の量は

$$1500\times4=6000(\mathrm{cm^3})$$

(2)蛇口Xから出る水の量は毎分3750$\mathrm{cm^3}$であるから、

$$3750\div1500=2.5$$

よって蛇口Xだけ開いているとき、水の高さは毎分2.5$\mathrm{cm}$ずつ減っていく。

(1)から、蛇口Aを開いたとき水の高さは毎分4$\mathrm{cm}$ずつ増えていくことが分かっているので、蛇口Aと蛇口Xを同時に開いたとき

$$4-2.5=1.5$$

であるから、毎分1.5$\mathrm{cm}$ずつ増えていく。

さて、グラフから高さ(ア)のとき時間は10分であるから、

$$1.5\times(10-4)=1.5\times6=9$$

よって4分のときより9$\mathrm{cm}$増えるので$16+9=25\mathrm{cm}$である。

(3)グラフから、「蛇口Aを閉じ、蛇口Yを開く」操作から5分で水の高さは

$$25-9=16\mathrm{cm}$$

減っている。よって水の高さは毎分$16\div5=3.2\mathrm{cm}$ずつ減っていることが分かる。

(2)から蛇口Xだけ開くとき、水の高さは毎分1.5$\mathrm{cm}$ずつ減っていくことが分かっているので、蛇口Yだけを開いたときの水の高さは

$$3.2-1.5=1.7$$

より、毎分1.5$\mathrm{cm}$ずつ減っていくことが分かる。

以上より、求める水の量は

$$1500\times1.7=2350\mathrm{cm^3}$$

である。

(4) (1)～(3)からそれぞれの蛇口を開いたときの水の高さの増減は

蛇口A:毎分$4\mathrm{cm}$ずつ増える

蛇口X:毎分$1.5\mathrm{cm}$ずつ減る

蛇口Y:毎分$1.7\mathrm{cm}$ずつ減る

よって、全ての蛇口を開いたとき、水の高さは毎分$4-1.5-1.7=0.8\mathrm{cm}$ずつ増えていく。

水槽の深さは問題より40$\mathrm{cm}$だから、水の高さが$40-9=31\mathrm{cm}$増えるのにかかる時間を調べればよい。

$$31\div0.8=\dfrac{310}{8}=38\ \dfrac{3}{4}\ (\text{分})=38\text{分}45\text{秒}$$

よって、全ての蛇口を開けてから38分45秒後に水槽がいっぱいになる。

全ての蛇口を開けたのは、最初に蛇口Aを開いてから13分のことなので、

求める時間は

$$13\text{分}+38\text{分}45\text{秒}=51\text{分}45\text{秒}$$

である。