問3の解き方を教えてください🙇‍♀️

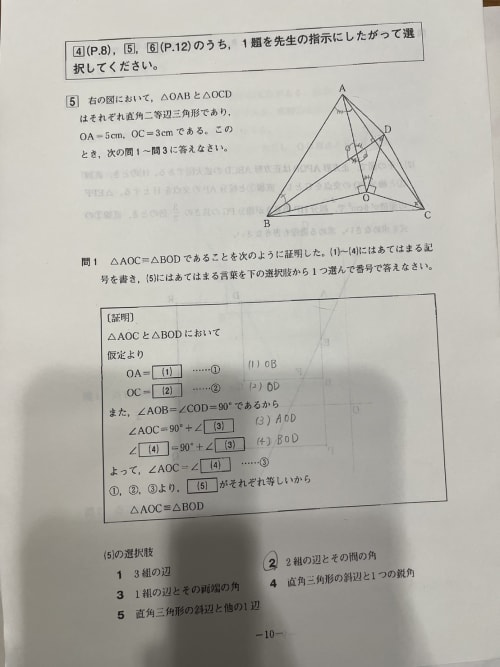
これは、まず立式からしますと、$△OBCの面積をSとすると、$

$$S=(四角形ABCD)-(△ABO)-(△DOC)-(△AOD)$$

また特殊な四角形の計算について考える必要がありますね。今回の問題で大事な$のは、四角形ABCD,△AODの面積です。$

$まず四角形ABCDにつ$いて、そのために情報集めをしますが、必要なのは対角線、$ACとBDだけで$す。もしかしたら知っているかもしれませんが、対角線が直交するとき、その四角形の面積はひし形と同じように

$$(面積)=(対角線1)(対角線2)÷2$$

でいいんです。一応軽く証明しておきますが「知っとるわ」というかたは飛ばしてください(下図参照)

したがって、合同の条件で、AC=BDであることから

$(△ABCDの面積)＝7×7÷2=\dfrac{49}{2}$

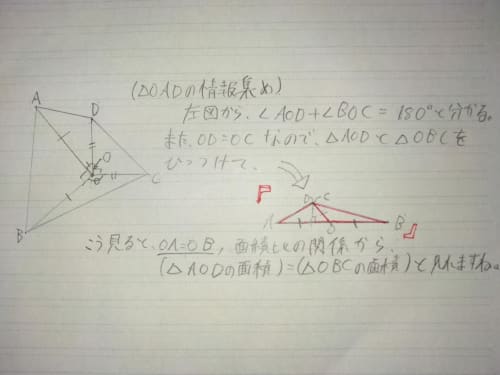
次は、$△AOD$について、これも複雑なので(下図参照)とさせてもらいます。すみません🙇図の通り、この面積は$△OBC,つまりS$に等しくなります

さて、必要なものはそろったので、問題の面積を出したいと思います。

$$S=\dfrac{49}{2}-S-\dfrac{25}{2}-\dfrac{9}{2}$$

$$∴(△OBCの面積)=\dfrac{15}{4}$$

以上です、もし万が一ですが値が間違っていると気づいた場合は教えてください。長い解説に目を通してくれて感謝します！