弦の基本振動・固有振動の解説|線密度と張力で決まる弦の波の速さの導出
この記事では,弦の微小振動や固有振動について解説します。弦の振動の伝わる速さを導出したのち,弦の振動の振動数や波長について考えてみます。また,1次元波動方程式との関連についても解説します。
弦の基本振動・固有振動とは
弦の基本振動・固有振動とは
以下のような両端が固定された弦を考えます。この弦を引っ張って離したとき,弦はどのような運動をするでしょうか。
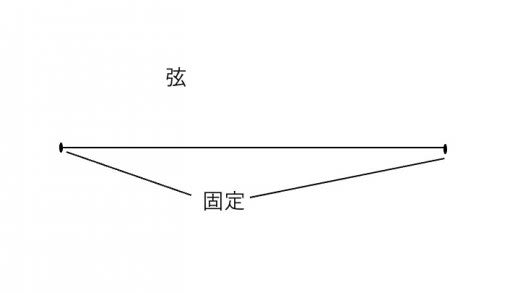
弦の運動は引っ張る位置によって様々ですが,十分時間が経つと以下のような種類の正弦波の重ね合わせになることが知られています。(理由は後述)

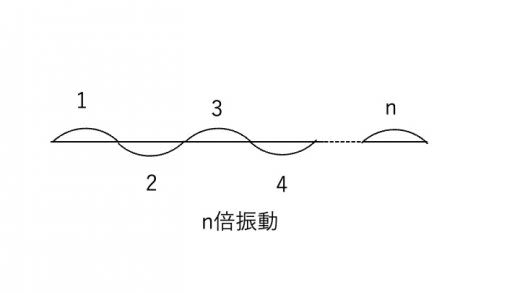
上のように腹が1つだけの振動を基本振動,腹が2つの振動を2倍振動,一般に腹がn個ある振動のことをn倍振動と呼びます。またこれらの振動のことを総称して,固有振動と呼びます。
この記事に関連するQ&A
弦を伝わる波の速さの導出〜次元解析〜
弦を伝わる波の速さの導出〜次元解析〜
次に弦を伝わる波の速さについて考えます。弦を伝わる速さを導出するのは,一見掴みどころのない問題ですが,各物理量の単位に着目することで求めることができます。
まず,弦の運動の性質を決定する物理量について考えてみましょう。そのような物理量は,弦の張力 と線密度 だと予想されます。よって弦を伝わる波の速さ も,これらの物理量で表すことができそうです。ここで, が と のみに依存すると仮定して,各物理量の単位に注目してみます。
の単位 :
の単位 :
の単位 :
ここで とすると左辺と右辺で単位が等しいので,
よって,
これらを解いて となります。よって となります。比例係数は1であることが知られているので, がわかりました。
このように,各物理量の単位(または次元)に着目して,求めたい物理量の表式を考えることを,次元解析と言います。
弦の固有振動数と波長
弦の固有振動数と波長
弦の長さを として,各固有振動の波長や振動数を求めてみましょう。
まず基本振動について,正弦波は腹2つ分で1周期なので,明らかに基本振動の波長は となります。また振動数については,公式 を用いて, となります。
同様にして,n倍振動の波長や振動数も求めてみましょう。n倍振動では半波長が の長さの中に,n個入っていると考えて, が成り立ちます。よって となります。また,振動数については となります。これらの結果は の時は上で求めた基本振動数の結果と一致します。固有振動の振動数のことを一般に固有振動数と言います。
固有振動の例題
固有振動の例題
弦楽器は弦を振動させることで振動数に応じた高さの音を出す。上で求めた固有振動数の表式を考えると,弦書きの音を高くするにはどうすれば良いか。
弦の固有振動数は で与えられる。この式より,弦楽器の音の高さ(振動数の大きさ)は
- (弦の長さ)が短いほど
- (線密度)が小さいほど
- (張力)が大きいほど
高くなることがわかる。
弦に関連する物理量をどのように設定するかは実際の弦楽器においても重要です。これらの性質が成り立つことを,実際にギターなどで実験してみてください。
下のように,糸の右端に質量 のおもりがつけられ,糸が張られた系がある。糸の線密度を とする。また,糸の左端から,滑車までの距離を とする。
(1)弦を弾くと基本振動が起こった。この時基本振動数 を求めよ。
(2)おもりの質量を にして弦を弾くと2倍振動が起こった。この時の振動数 は の何倍か。
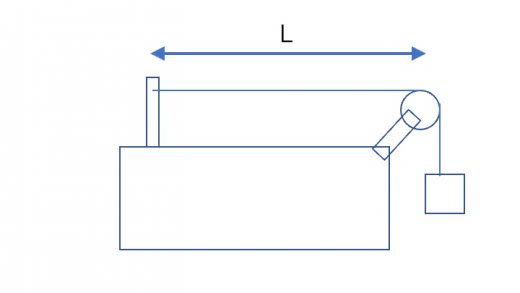
(1)糸の張力 は,おもりと糸の力のつりあいより, である。よって上で求めた固有振動の式で として, を得る。
(2)(1)と同様にして,( に注意して) を求めると, となる。よって を得る。
弦と1次元波動方程式
弦と1次元波動方程式
振動現象は波動方程式という偏微分方程式で記述されます。以下では微小振幅の弦について1次元波動方程式を導き,固有振動や波の速さ が自然に説明されることを確かめます。
微小振幅の弦の変位 について以下の式が成り立つ。
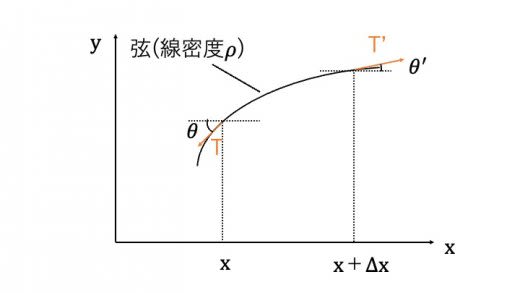 上の図のように座標,物理量を設定して, 方向, 方向の運動方程式を考える。弦の振動は横波なので, 方向の加速度は0である。
上の図のように座標,物理量を設定して, 方向, 方向の運動方程式を考える。弦の振動は横波なので, 方向の加速度は0である。
方向:
方向:
弦の振幅が微小であることから,上の図で は微小角である。よって , などと近似できる。 より 両辺を でわり とすると
となるので結論の式を得る。
一般の振動の1次元波動方程式は,波の速さ を用いて,以下のようになることが知られています。
この式と,微小振幅の弦の式を比べると,確かに が成り立っていることがわかります。
また,固有振動は,実は1次元波動方程式の解であり,1次元波動方程式の一般解は,固有振動の重ね合わせによって表されることが知られています。よって弦の振動も固有振動の重ね合わせとなります。
大学では「ダランベールの解法」や「因数分解法」を用いて1次元波動方程式を実際に解き,弦の振動をもっと詳しく調べます。











