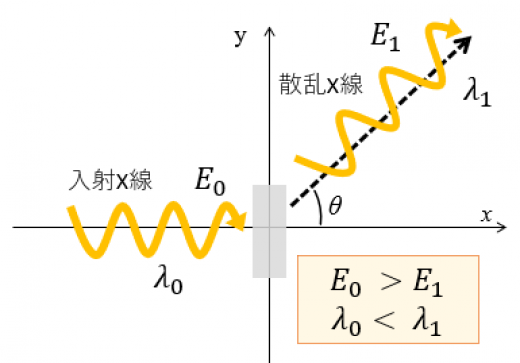
コンプトンは, 散乱前後の波長の伸び Δλ がどのくらいか計算で求めようとしました。そのためにコンプトン散乱において, 以下のことが成り立つと考えます。
- X線を光子という粒子の流れと考える(光の粒子性)
- X線の光子1個が電子1個に衝突する場合を考える
- 衝突前後で, エネルギー保存則と運動量保存則が成り立つと考える
上記の仮定のもと, Δλ を求めるために以下のように計算を進めていきます。
光子の運動量の導出方法
まず, 光子の運動量について考えます。一般に運動量 p は速度 v と質量 m を用いて,
p=mv
となります。光子は光速 c の速度で運動します。ここで問題なのが, 光子は質量を持たないという点です。光子の運動量を表すために以下のような式変形を考えます。
光子1個のエネルギーを Ep[J] , プランク定数を h[J⋅s] , 光子の振動数を ν[Hz] , 光子の波長をλ[m], 光速 c[m/s] とすると,
Ep=hν=λhc
という関係が成り立ちます。また, 光子1個の質量を mp と仮定し, 相対性理論の式 E=mc2 を左辺に代入すると,
mpc2mpc=hν=chν
となります。mpc は運動量を表すので, 光子1個の運動量 pp は質量 mp を用いず,以下のように書くことができます。
光子1個の運動量
pp=chν=λh
エネルギー保存則と運動量保存則を考える
コンプトンは, コンプトン散乱前後でエネルギー保存則と運動量保存則が成り立つと考えました。
X線の光子1個が物質中の電子1個に衝突し, 跳ね飛ばす場面を考えます。
エネルギー保存則
X線線のエネルギーは λhc, 電子の運動エネルギーは 21mv2 となります。電子は衝突前は静止しているため, 運動エネルギーがありません。
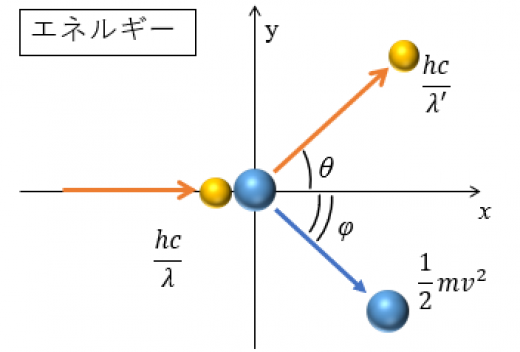
以下のようなエネルギー保存則が成り立ちます。
λhc+0=λ′hc+21mv2
以後の計算で使いやすくするために, 式変形し, 両辺に 2m をかけると,
21mv2(mv)2=λhc−λ′hc=2m(λhc−λ′hc)
となります。この式を①とします。
運動量保存則
次に運動量保存則について考えます。光子と電子が衝突後, 光子はx軸に対して角度 φ で, 電子は角度 φ で散乱します。
そのため, 運動量をx軸(入射X線方向)とy軸(入射X線と垂直方向)に分解して, それぞれの方向で運動量保存則が成り立つと考えます。
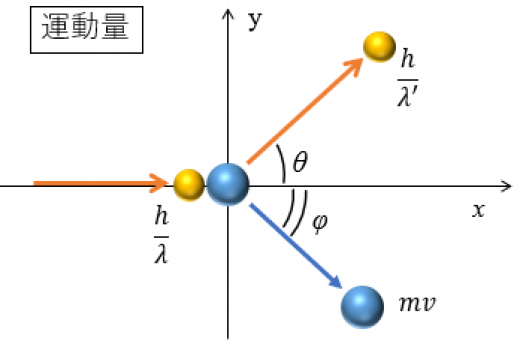

x方向(入射X線方向)の運動量保存則は以下のようになります。
λh+0=λ′hccosθ+mvcosφ
y方向(入射X線と垂直方向)の運動量保存則は以下のようになります。
0=λ′hcsinθ−mvsinφ
2式を変形します。x方向の運動量の式を変形し, 両辺を二乗します。
mvcosφ(mv)2cos2φ=λh−λ′hcosθ=(λh−λ′hcosθ)2
同様にy方向の運動量の式を変形し, 両辺を二乗します。
mvsinφ(mv)2sin2φ=λ′hsinθ=(λ′hsinθ)2
変形した2式の和を取り, cos2φ+sin2φ=1 を用いると,
(mv)2cos2φ+(mv)2sin2φ(mv)2=(λh−λ′hcosθ)2+(λ′hsinθ)2=(λh−λ′hcosθ)2+(λ′hsinθ)2
となります。この式を②とします。
波長の伸び Δλ の導出
エネルギー保存則から求めた①と運動量保存則から求めた②を等号で結ぶと,
2m(λhc−λ′hc)=(λh−λ′hcosθ)2+(λ′hsinθ)2
が成り立ちます。右辺の各項を h2 でくくると,
2mhc(λ1−λ′1)=h2(λ1−λ′1cosθ)2+h2(λ′1sinθ)2
となります。両辺を h2 で割り, cos2θ+sin2θ=1 を用いると,
h2mc(λ1−λ′1)=(λ1−λ′1cosθ)2+(λ′1sinθ)2=(λ1)2−2(λ1)(λ′1cosθ)+(λ′1cosθ)2+(λ′1sinθ)2=(λ1)2−2(λ1)(λ′1cosθ)+(λ′1)2
となります。ここで, 右辺に +2(λ1)(λ′1)−2(λ1)(λ′1) を加えると*,
h2mc(λ1−λ′1)=(λ1)2+(λ′1)2−(λλ′2cosθ)+2(λ1)(λ′1)−2(λ1)(λ′1)=(λ1−λ′1)2+λλ′2(1−cosθ)
となります。
*この操作を行った理由は, (λ1−λ′1)2 を作るためです。
上式のカッコ内を計算しすると,
h2mc(λλ′λ′−λ)=(λλ′λ′−λ)2+λλ′2(1−cosθ)
となります。ここで, λ と λ′ の差は極めて小さく, (λ−λ′)2≈0 であると考えます。ただし, λ−λ′=0 です。光子の運動量を表すために以下のような式変形を考えます。
すると, 上式の右辺第一項は消えて, 以下のように計算ができます。
h2mc(λλ′λ′−λ)hmc(λ′−λ)(λ′−λ)=(λλ′λ′−λ)2+λλ′2(1−cosθ)=(1−cosθ)=mch(1−cosθ)
ここで, 波長の伸びを Δλ=λ′−λ と置くと,
コンプトン効果における波長の伸びは以下のように決まります。
コンプトン効果における波長の伸び
Δλ=mch(1−cosθ)
-
プランク定数 h=6.6×10−34[J⋅s]
-
光速 c=3.0×108[m/s]
-
粒子の質量 m[kg]
コンプトンの功績
コンプトンは, 計算で求めた波長の伸び Δλ と, 実験で測定した入射X線と散乱X線の差がよく一致していることを確認しました。
したがって, X線を光子の流れと捉え, エネルギー保存則や運動量保存則が成り立つと考えられることを証明しました。(光の粒子性)
当時, 光電効果の発見により証明されつつあった光量子仮説(光が波動かつ粒子である)を後押しする結果となりました。
→光電効果
電子のコンプトン波長
コンプトン効果における波長の伸び
Δλ=mch(1−cosθ)
の右辺においてh,m,cは定数のためコンプトン効果における波長の伸びは散乱角 θ に依存します。
散乱角 θ が大きくなるにつれて, Δλ は大きくなります。散乱角 θ=2π の場合の Δλ をコンプトン波長といいます。
また, 電子の質量 me=9.1×10−31[kg] を用いて, このときのコンプトン波長(θ=2π)について考えると, 以下のようになります。
Δλ=(9.1×10−31)×(3.0×108)6.6×10−34×(1−0)=9.12.2×10−11≃2.4×10−12
Δλ=2.4×10−12[m] は電子のコンプトン波長といいます。
コンプトン散乱におけるエネルギー保存則と運動量保存則(成分分割)は頻出の問題のため, よく復習しておきましょう。