有界とは何か～上界・上限と下界・下限

更新 2023/08/22

有界の定義

実数の集合 $A$ に対して $A$ が有界であるとは，
「ある実数 $m,M$ が存在して，任意の $x\in A$ に対して $m\leqq x\leqq M$ 」となることを意味する。
$A$ 上の関数 $f$ が有界であるとは， $f(A) = \{ y \mid \exists x \in A , f(x) = y \}$ が有界であることを意味する。

この記事では，漠然と使いがちな有界性にまつわる用語を厳密に説明していきます。

sup(上限)とinf(下限)の意味，max・minとの違いも参考にしてください。

実数の部分集合の有界性

上界・上限・最大値実数の部分集合 A⊆RA\subseteq\mathbb{R}A⊆R に対して
実数 MMM を
任意の x∈Ax \in Ax∈A に対して x≦Mx \leqq Mx≦M
となるように取れるとき，AAA は上に有界である といいます。
上に有界な集合 AAA に対して，特殊な実数に名前をつけましょう。
定義
任意の x∈Ax\in Ax∈A に対して x≦yx \leqq yx≦y となる実数 yyy を上界 という。
上界の中で最小のものを上限といい，sup⁡A\sup AsupA と書く。
AAA の元の中で最大のものが存在するとき，最大値といい，max⁡A\max AmaxA と書く。
AAA 上の関数 fff の上界・上限・最大値をそれぞれ f(A)f(A)f(A) の上界・上限・最大値と定める。
例上に有界な集合に対して，上限は必ず存在しますが，最大値は存在しないことがあります。
開集合 I1=(1,2)={x∈R∣1<x<2}I_1 = (1,2) = \{ x \in \mathbb{R} \mid 1 < x < 2 \}I1​=(1,2)={x∈R∣1<x<2} は上に有界です。
上界は 222 以上の任意の実数です。
上界のうち最小のものは 222 なので，上限は 222 です。
I1I_1I1​ の元はいくらでも 222 に近く取れます。しかし，222 自体は I1I_1I1​ の元ではないです。よって最大値は存在しません。
閉集合 I2=[1,2]={x∈R∣1≦x≦2}I_2 = [1,2] = \{ x \in \mathbb{R} \mid 1 \leqq x \leqq 2 \}I2​=[1,2]={x∈R∣1≦x≦2} は上に有界です。
上界は 222 以上の任意の実数です。
上界のうち最小のものは 222 なので，上限は 222 です。
I2I_2I2​ の元は 222 を越えることはないです。一方 222 は I2I_2I2​ の元であるため，最大値は 222 です。
例から予想できるように，最大値が存在するとき max⁡A=sup⁡A\max A = \sup AmaxA=supA となります。
下界・下限・最小値実数の集合 AAA に対して
実数 mmm を
任意の x∈Ax \in Ax∈A に対して m≦xm \leqq xm≦x
となるように取れるとき，AAA は下に有界である といいます。
上に有界なとき同様に，下に有界な集合に対してもいくつかの実数に名前をつけます。
定義
任意の x∈Ax\in Ax∈A に対して y≦xy \leqq xy≦x となる実数 yyy を 下界 という。
下界の中で最大のものを下限といい，inf⁡A\inf AinfA と書く。
AAA の元の中で最小のものが存在するとき，最小値といい，min⁡A\min AminA と書く。
AAA 上の関数 fff の下界・下限・最小値をそれぞれ f(A)f(A)f(A) の下界・下限・最小値と定める。
例下に有界な集合に対して，下限は必ず存在しますが，最小値は存在しないことがあります。同じように例を考えればOKです。
開集合 I1=(1,2)={x∈R∣1<x<2}I_1 = (1,2) = \{ x \in \mathbb{R} \mid 1 < x < 2 \}I1​=(1,2)={x∈R∣1<x<2} は下に有界です。
下界は 111 以下の任意の実数です。
下界のうち最大のものは 111 なので，下限は 111 です。
I1I_1I1​ の元はいくらでも 111 に近く取れます。しかし，111 自体は I1I_1I1​ の元ではないです。よって最小値は存在しません。
閉集合 I2=[1,2]={x∈R∣1≦x≦2}I_2 = [1,2] = \{ x \in \mathbb{R} \mid 1 \leqq x \leqq 2 \}I2​=[1,2]={x∈R∣1≦x≦2} は下に有界です。
下界は 111 以下の任意の実数です。
下界のうち最大のものは 111 なので，下限は 111 です。
I2I_2I2​ の元は 111 を下回ることはないです。一方 111 は I2I_2I2​ の元であるため，最小値は 111 です。
最大のときと同様に，最小値が存在すると min⁡A=inf⁡A\min A = \inf AminA=infA となります。
数式による特徴付け上限・下限の性質を数式による特徴付けます。ε\varepsilonε-δ\deltaδ 論法などと組み合わせて，応用する際に有用です。
上限上限の特徴づけ
MMM が AAA の上限であることは，次の2つを満たすことと同値：
任意の x∈Ax \in Ax∈A  に対して M≧xM \geqq xM≧x
ε>0\varepsilon > 0ε>0 を任意に取ったとき，ある x∈Ax \in Ax∈A があって M−x<εM - x < \varepsilonM−x<ε となる。
2つ目の条件は，上限にいくらでも近い元 x∈Ax\in Ax∈A の存在を主張しています。
例えば I1=(1,2)I_1 = (1,2)I1​=(1,2) の上限を考えるとき，2.12.12.1 は ε=0.1\varepsilon = 0.1ε=0.1 とすると，任意の x∈(1,2)x \in (1,2)x∈(1,2) に対して 2.1−x>2.1−2=0.1=ε2.1 - x > 2.1 - 2 = 0.1 = \varepsilon2.1−x>2.1−2=0.1=ε となってしまい，上限とならないことが分かります。
下限下限の特徴づけ
mmm が AAA の下限であることは，次の2つを満たすことと同値：
任意の x∈Ax \in Ax∈A  に対して m≦xm \leqq xm≦x
ε>0\varepsilon > 0ε>0 を任意に取ったとき，ある x∈Ax \in Ax∈A があって x−m<εx - m < \varepsilonx−m<ε となる。

平面や空間の有界性

平面上の集合が有界であるとは，どのように定義すると良いでしょうか？
上の図の左は「有界だなぁ」と感じるでしょう。その直観をどのように定義に落とし込むとよいでしょうか。2種類の同値な定義を紹介します。
定義１平面上の点に最大値・最小値のようなものを考えるのは難しそうです。しかし，困難は分割せよというように，xxx 軸・yyy 軸（・zzz 軸）に分けて大小を見ることで，有界性を定めることができます。
平面の有界１
xyxyxy 平面上の集合 AAA に対して，
平面上の点 (m1,m2),(M1,M2)(m_1 , m_2) , (M_1 , M_2)(m1​,m2​),(M1​,M2​) を
任意の (x,y)∈A(x,y) \in A(x,y)∈A に対して m1≦x≦M1m_1 \leqq x \leqq M_1m1​≦x≦M1​，m2≦y≦M2m_2 \leqq y \leqq M_2m2​≦y≦M2​
となるように取れるとき，AAA は有界である という。（xyzxyzxyz 空間のときも同様に考える。）
先ほどの図での例を見てみましょう。
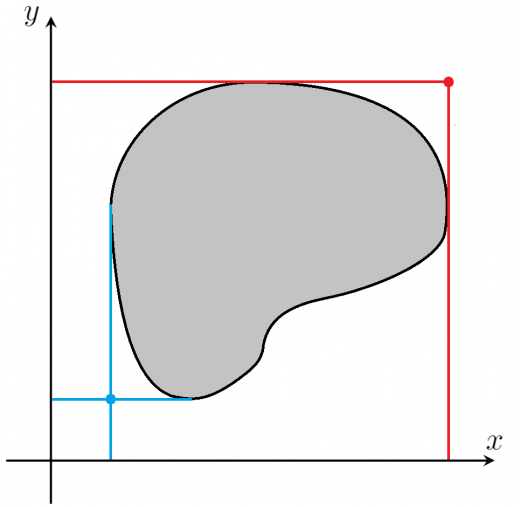
定義２視点を変えることで異なる定義をすることもできます。
実数における有界な集合には，上界と下界が存在しますが，これらの差の絶対値を取ると「どれくらいの距離があるのか」がわかります。有界な集合を「距離が有限な集合」だと思うと次のような定義は自然でしょう。
平面の有界２
平面（より広く空間）の集合 AAA が，半径が有限な円（空間の場合は球）で覆えるとき，有界であるという。
先ほどの図での例を見てみましょう。
2つの定義の同値性これら2つの定義は同値になります。
証明（平面版）
1⇒21 \Rightarrow 21⇒2
定義中の (m1,m2),(M1,M2)(m_1 , m_2) , (M_1 , M_2)(m1​,m2​),(M1​,M2​) を直径とする円を取れば AAA を覆うことができる。
2⇒12 \Rightarrow 12⇒1
AAA を中心 (x0,y0)(x_0,y_0)(x0​,y0​) 半径 rrr の円で覆えたとする。
このとき円盤内の任意の点 (x,y)(x,y)(x,y) に対して x0−r≦x≦x0+rx_0 - r \leqq x \leqq x_0 +rx0​−r≦x≦x0​+r，y0−r≦y≦y0+ry_0 - r \leqq y \leqq y_0 +ry0​−r≦y≦y0​+r である。
AAA は円に覆われることから，AAA の元 (x,y)(x,y)(x,y) を任意に取ったとしても同様の不等式が成立する。
平面上の有界な集合の例パラメーターが付いた平面上の曲線 c(t)  (a≦t≦b)c(t) \; (a \leqq t \leqq b)c(t)(a≦t≦b) が閉曲線であるとは，c(a)=c(b)c(a) = c(b)c(a)=c(b) であることを意味します。
閉曲線で囲まれた集合は有界です。
実際，c(t)=(c1(t),c2(t))c(t) = (c_1 (t) , c_2 (t))c(t)=(c1​(t),c2​(t)) とおいたとき，(m1,m2)(m_1 , m_2)(m1​,m2​)，(M1,M2)(M_1 , M_2)(M1​,M2​) として，(min⁡c1(t),min⁡c2(t))(\min c_1 (t) , \min c_2 (t))(minc1​(t),minc2​(t)) と (max⁡c1(t),max⁡c2(t))(\max c_1 (t) , \max c_2 (t))(maxc1​(t),maxc2​(t)) を取れば，これらは条件1  を満たします。

展望

ここまでは，実数の集合について有界性・上界・上限・最大などを考えましたが，より一般の集合についても考えることができます。そのためには，集合の要素の間の「比較方法」を考える必要があります。

実数と不等号のように，集合と比較方法のペアを順序集合といいます。

平面の有界性の定義1は順序集合の直積に関係し，定義2は不等号として包含関係を用いたものと解釈できます。

これらは束論などのトピックに繋がっていきます。興味がある人は是非調べてみてください。

記事中で紹介したもの以外で有界になる条件を考えてみてください。例えば，平面上の集合の周長ではうまくいきません。有界でも周の長さは無限大の例については「フラクタル」を調べてみましょう。