【中学レベル】数学の難問おすすめ3選!解き方や難問対策のための勉強法も紹介!
「中学レベルの数学の難問には、どのような問題なのか?」
「難問の解き方・難問対策のための勉強法は?」
このような疑問を感じた方もいるでしょう。
数学の難問にはどのような内容になっているのか、気になるはずです。
この記事では中学レベルの数学の難問について、おすすめ3選を紹介していきます。
また、難問の解き方・難問対策のための勉強法も解説していきましょう。
この記事を読み終わった方は、難問を解いてみようと考えるはずです。
数学の難問おすすめ3選についてざっくり説明すると
- 難問を解くためには基礎力が必要となる
- 「思考力」「根性」「計算スピード」が難問を解くと身につく
- 難問は解けなくても大丈夫
難問の対策は必要?

ここでは、 中学レベルの数学の難問に対策が必要なのか紹介していきます。
高校入試に難問は出題される?
数学の難問はレベルによって異なりますが、レベルの高い私立学校の高校入試では出題される可能性があります。このような学校の高校入試を検討している方は難問の対策をするべきです。
毎年、難問が出題されている学校を受験する場合は、過去問を解く必要があるでしょう。しかし、高校によっては難問を必ず解く必要がない学校もありますので、事前に確認しておくと良いです。
難問に関してはある程度は解ける方が良いでしょう。そのため、難問を解ける方の特徴・経験を調べて集めたデータを分析して対策方法を考えるようにしましょう。
基礎からの積み上げで対策
高校入試などの受験で必要となるレベルの難問の場合、試験対策をしていくと解けるようになる方が多いです。最初は難しいと感じる方もいますが、問題を解いていくうちに自然と解けるようになるでしょう。
受験用の問題集・対策を完璧に解けるようになれば、数多くの問題が解けるようになります。まずは基本の問題から解いていき、基礎を固めていきましょう。そして、応用の問題も解けるようになっていくはずです。
難問を解くためには、基礎をしっかりと固める必要があります。毎日、継続的に問題を解いて基礎を固めて難問が解けるように対策をしましょう。
難問を飛ばす力が大事?
高校入試などの受験では、試験当日に点数をできるだけ多く取る必要があります。
そのためには、まず分かる問題を解けるようにしていき、確実に得点を重ねていきましょう。
これは分からない問題・時間がかかってしまう問題に関しては、わざと解かない方法を考える必要があると言えるでしょう。受験者が解けないような難問を思い切って解かずに、飛ばすことも大事です。
上記のようなことを考えて、難問以外のレベルの問題はしっかりと解けるように勉強をする必要があります。確実に解ける問題を増やして、試験当日に良い点が取れるようにしましょう。
本当の難問は解けなくていい?
数学はある程度のレベルに達すると、素質が大きく影響してくるでしょう。更に、向き・不向きが出てくるため、すぐに難問が解ける方も存在します。このように直感的に解ける「天才」と呼ばれる方もいるのです。
「天才」と呼ばれる子供は並外れた才能を持っております。そのため、その子供と同じレベルになることは、難しいでしょう。仮に日々、努力を積み重ねたとしても同じレベルになれる方はごく僅かです。
必ず難問を解けるような方になる必要はなく、受験に成功できるレベルの能力を身につければ良いのです。自らができる受験対策を行えば大丈夫なので、安心しましょう。
難問を解くメリット

数学の難問は学校のテストで出題されることはありません。また、大学受験でも難問が出題されることは少なくなっています。このことから、難し過ぎる問題に関しては解ける必要はないと言えるでしょう。
ただ、難問を解くことができると多くのメリットがあります。例えば、「思考力」「根性」・「計算スピード」などの能力を身につけることができます。
もし、難問が解けるようになれば、自分にとってプラスになることもあるのです。
難問に挑戦するのであれば、中学1年生・2年生で時間が空いている時が良いでしょう。また、難問には論理パズルな問題があり、数学の要素が少ないものもあります。その場合は、友人とクイズをする感覚で解いてみましょう。
中学生数学の難問厳選3問!
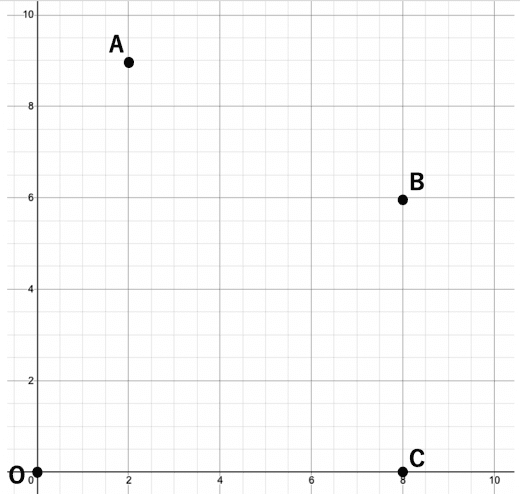
それでは、ここで中学生数学の難問かつ良問である、以下の問題にチャレンジしてみましょう。
上の図のように、4点 を頂点とする四角形 がある。
このもとで、以下の問いに答えなさい。
- 三角形OABの面積を求めよ
- 点 を通り、かつ三角形 の面積を2等分する直線の方程式を求めよ
- 点 を通り、四角形 の面積を3等分する2本の直線の式をそれぞれ求めよ。
それでは、以下ではこの問題の解答解説をお伝えします。
三角形ABCの面積を求めよ
この問題は初級レベルです。
以下の図のように点 を定めてあげれば、あとは単純な引き算で面積を求めることができます。
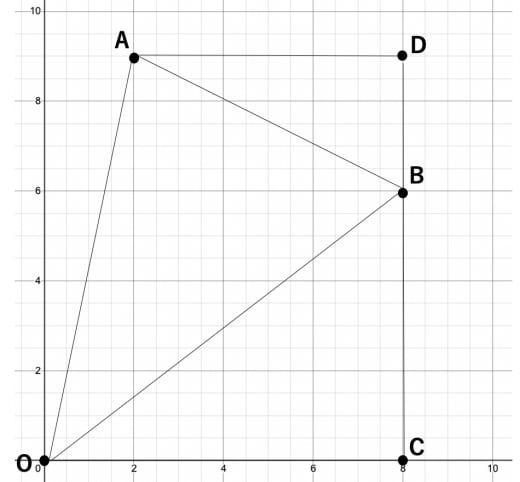
求める三角形 の面積を とすると
点Aを通り、かつ三角形OABの面積を2等分する直線の方程式を求めよ
この問題は初級〜中級レベルです。
1問目で の面積が だと求められましたが、この数字を使って「面積が の三角形を2つ作ろう」と考えると、かなりややこしいことになってしまいます。
実は上で求めた は、この問題を解くためには一切必要ありません。
以下のように辺 の中点を とすると、 と の面積は等しくなることが分かります。底辺の長さ( または )が等しく、高さも等しいからです。
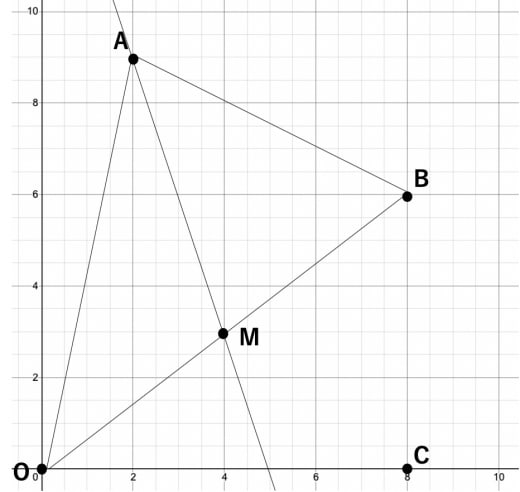
したがって、直線 の式を求めれば良いだけとなります。
と の2点を通る直線は傾きが
切片を として、 に、 を代入して、
したがって直線 は
点Bを通り、四角形OABCの面積を3等分する2本の直線の式をそれぞれ求めよ
最後の問題は難しく、本番試験で出てきたら焦ってしまう人も多いかと思います。
2問目では という数字を用いずに解答しましたが、今回はバリバリに数字を使います。
以下のように、求める2本の直線が辺 及び辺 と交わる点をそれぞれ とします。
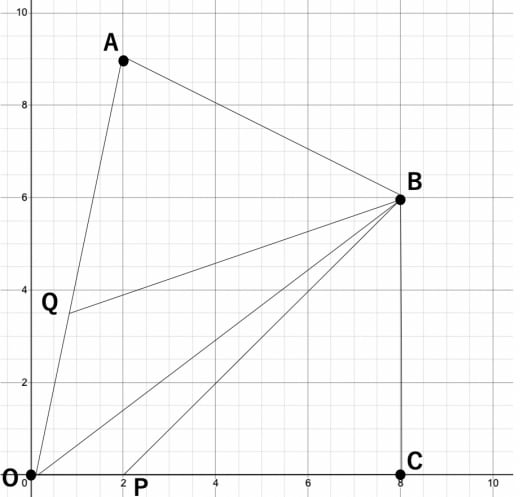
まず、問題1より
そのため四角形 を三等分した面積は
つまり、 の面積が なので、
よって
つまり、 であることが分かります。
次に の座標を求めます。四角形 であり、かつ三角形OBPの面積は三角形OBCの面積から三角形BCPの面積を引けば良いので、
つまり、 の面積は
、なので、
つまり の 座標および 座標は の座標のそれぞれ倍なので
これで の座標と の座標がそれぞれわかったので、あとは直線 と直線 の式を導出するだけです。
その計算は割愛しますが、答えはそれぞれ以下のようになります。
直線 :
直線 :
難問を解くためのスキル・能力は?

続いて、数学の難問を解くために必要となるスキル・能力について紹介していきます。
試行錯誤の速度が早い
難問を解くためには1つの方法ではなく、多角的なアプローチの方法をインプットする必要があります。そして、実際に難問を解く際にインプットした多角的なアプローチを試していきましょう。
例えば、最初の方法を試してみて上手くいかなかった場合は、新たな方法を行うという流れです。もし、問題を解いていて解けないと分かった際は、見切る力などが大事になります。
更に先を見通す力も必要となり、その場で的確な判断をするようにしましょう。このように的確な判断を行うためには、多くの問題を解いて解法・流れをしっかりと理解しておくと良いです。
多角的思考
1つの問題を解く際には、多角的なアプローチを行うようにしましょう。これは多くの問題・レベルの高い問題を解いていると、複数の解き方があることを把握できます。
また、多角的なアプローチができるようになっていくと、過去に解いた問題と似たような問題が出題された場合、解き方を選択できるようになります。
今まで、同じ解き方しかできなかった方が、多角的なアプローチを行えると多くの問題が解けるようになるでしょう。
難問を解くためには、基礎の解法を組み合わせで解いていきます。問題の演習で覚えた解法が多いほど、難問が解きやすくなるでしょう。
人と解説をシェアする
もし、難問を解く際に自分と同レベルの友人がいれば、難問を紹介し合うと良いです。また、解説・解釈について話し合うことで、今まで気付かなかった見方・考え方など新しいものを知ることができます。
この方法を取るとお互いの理解も深まるため、可能であれば試してみましょう。
演習量が大事
高校入試など受験で出題される難問に関しては、解き方にパターンがあります。受験で点数を少しでも多く取るために基礎の勉強をしっかりとしましょう。そして、応用の解き方を覚えるようにすると良いです。
やはり、多くの演習量が大事になり、そこから基礎の解き方を覚えていきましょう。1問でも多く解くことで、自分が覚える解き方も自然と増えていくはずです。
有名な難問は解き方の手掛かり掴みにくくなっているため、パズル・知恵の輪を解く感覚で行いましょう。難問を解くための対策は難しくなっているので、ゲームの感覚で解くと良いです。
図形問題は別解のアプローチが多数
難問が解けた時に用いた解法に時間がかかったり、計算量が多い場合は達成感があるはずです。ただ、問題が解けた達成感を味わえなかった場合は、必要以上の手間のかかる方法で計算を行っているはずです。
このような場合は、難問を解く方法として別の方法があると考えましょう。せっかく問題が解けたとしても、高校入試などの受験の際に時間がかかってしまっては良い点を取ることはできません。
難問を解く時は、多角的なアプローチをしていきましょう。特に、図形問題はアプローチの方法が多くなっています。そのようにアプローチをしないと図形問題を解くことができないでしょう。
多角的なアプローチから図形問題を解くようにしていくと良いです。
東大生が伝授する数学の勉強法や、テスト対策について知りたい方は、以下の記事を参考にしてください。
中学生向けの難問の探し方

最後に、中学生向けの難問の探し方にについて、紹介していきます。中学1年生・2年生から難問を解いてみることをおすすめしますが、どこから探せばよいのか見ていきましょう。
志望校の過去問にふれる
中学生が高校入試でレベルの高い問題が出される学校を受験する際は、その学校で出題された過去問を解くと良いです。実際に出題されていた問題を解くことで、問題の出題傾向・対策方法も知ることが可能になります。
受験で難問を解くためには、過去の難問を解いて慣れていくことが重要です。また、受験用の難問は解き方にパターンがあるため、解いて確認する必要があります。
レベルの高い高校を目指す中学生は、早い段階から難問を解くと良いです。日頃から基礎を固めながら、難問を解くための方法を覚えるようにしましょう。
特に受験を控えている中学生は、しっかりと対策をするように必要があります。
難問のまとめサイト
中学生で数学の難問を解きたい場合は、インターネットで探してみると良いです。インターネットでは多くの難問が載っているため、解いてみたい問題を選んでみましょう。
しかし、中学生の知識で解ける難問でも本当は高校生のレベルで解く問題が多くなっています。学校でしっかりと勉強した中学生でも解けないようなレベルの問題があります。
いきなり、難し過ぎる問題を中学生が解こうとしても、自信を失ってしまうでしょう。そのため、インターネットの難問は遊びの感覚で解くと良いです。学校の成績に影響するわけではないため、気楽に解くようにしましょう。
通信教育の発展問題は難問がたくさん
通信教育の場合は学習がレベルごとに分かれており、発展学習の教材もあります。もし、基礎的な問題だけではなく難しい問題が解きたい場合は通信教育がおすすめです。
また、通信教育では難問が多くあるため、インターネットで自ら探す手間も省けるでしょう。効率的に難問を解きたい時は、通信教育で学習を進めるのも良いです。自らのレベルに合った難問を解くことが可能になります。
ただ、難問を解く場合は基礎を固める必要があるため、中学生は学校の教科書・問題集で勉強をしていきましょう。難問を解くためには基礎が大事になるので、中学生はしっかりと勉強して理解を深めると良いです。
通信教育を比較したい方は以下の記事をご覧ください。
中学レベルの数学の難問まとめ
数学の難問についてまとめ
- 難問は中学生1年生・2年生から取り組んでも良い
- 難問を解くためには演習量が大事
- 難問に慣れるなら過去問や通信教育がおすすめ
この記事では、中学レベルの数学の難問について、項目に分けて紹介してきました。
また、解き方・難問対策のための勉強法も解説してきました。
難問・図形問題を解くためには、多方向からアプローチをする必要があります。
この記事を読んで難問に興味を持った方は積極的に解いてみましょう。また、親子で難問を解こうと協力してみるのも良いでしょう。
是非自分なりの取り組み方で難問にチャレンジしてみてください!








