算数の公約数・最大公約数を完全解説!簡単な求め方や計算方法・センター試験対策も紹介
更新
「算数の公約数・最大公約数はどう教えれば良い?」
「簡単な求め方はある?より良い計算方法や公式は?」
などと疑問をお持ちの方もいるでしょう。
小学生の算数でわかりにくい概念の一つが、公約数・最大公約数です。ご自身では理解できるものの、お子さんにうまく教えられないという親御さんも多いでしょう。
今回は算数の公約数・最大公約数について、簡単な求め方や計算方法・公式、センター試験対策などを解説します。
これを読んで、小学生のお子さんに算数を教える上での参考にしてください。
算数の公約数・最大公約数についてざっくり説明すると
- 連除法を覚えると便利
- 高校数学ではユークリッドの互除法を使う
- 算数学習には通信教育がおすすめ
算数の公約数とは

まずは公約数の意味や公倍数との違いから見ていきましょう。
そもそも約数とは
約数とはある数をやり切ることができる整数(主に自然数)を指しますが、これはその数を掛け算で表した時に登場する数のことです。
例えば、18を自然数同士の掛け算で表すと以下の3パターン(順不同)が考えられます。
- 1×18
- 2×9
- 3×6
よって、18の約数は1、2、3、6、9、18です。これらは全て18を割り切ることができます。
公約数・最大公約数の意味
公(おおやけ)には「共有」という意味がありますが、公約数とは複数の数が共有する約数のことです。例えば、18と12の公約数を考えてみましょう。
上記の通り、18の約数は1、2、3、6、9、18です。一方で12は以下のような掛け算で表すことができます。
- 1×12
- 2×6
- 3×4
よって、12の約数は1、2、3、4、6、12です。この時、18と12の約数では1、2、3、6が共通しているので、これらが18と12の公約数ということになります。
またその中で最も大きい6が、18と12の最大公約数です。
公倍数・最小公倍数との違いは?
一方で倍数とはある数を整数倍(主に自然数倍)した数のことです。例えば、6の九九を考えてみると、6×1=6、6×2=12、6×3=18、6×4=24という風に続いていきます。この時、6、12、18、24などは6の倍数です。
同様に4×1=4、4×2=8、4×3=12、4×4=16、4×1=20より、4の倍数は4、8、12、16、20などになります。
また公倍数とは複数の数が共有する倍数のことを指すので、6と4の公倍数は12、24、36などです。さらにその中で最も小さい数が最小公倍数となるため、6と4の最小公倍数は12になります。
公約数の求め方

ここからは公約数の求め方について解説します。
最大公約数の求め方は?
最も単純な求め方は、先ほどのようにそれぞれの約数を書き出して見つけるという方法です。学習の初期段階において、公約数の概念を理解するためにはこの方法が役立ちます。
しかし、数が大きくなるとこの方法で最大公約数を求めるのは大変です。非常に時間がかかるため、問題を解く上ではおすすめしません。
最大公約数を素数・素因数分解から考える
数を素数に分解することを素因数分解と言いますが、これによっても最大公約数を求めることができます。
ちなみに素数とは1とそれ自身以外に正の約数を持たない自然数のことです。例えば、2、3、7、11などが素数になります。
素数を使った最大公約数の求め方ですが、それぞれの数を素数の掛け算に分解し、共通する素数を全て掛け合わせた数字が最大公約数です。
例えば、12と18をそれぞれ素因数分解すると以下のようになります。
- 12=2×2×3
- 18=2×3×3
上記のうち、共通する素数は2と3なので、12と18の最大公約数は2×3=6です。
連除法で簡単に計算できる!
最大公約数と最小公倍数を求めるのに便利な方法として連除法というのがあります。以下ではそのやり方を説明します。
まず最大公約数を求めたい2つの数を並べ、その左に両者を割り切れる最小の素数を書いてください。続いて割り算の答えを2つの数の真下に書き、同様の作業を2つの数が「互いに素」になるまで続けます。
なお、「互いに素」とは2つの数の公約数が1しかない(最大公約数が1)という状況のことです。
例えば、18と24を割り切ることができる最小の素数は2なので、2を18と24の左に書き、割り算の答えである9と12を18と24の下にそれぞれ書きます。
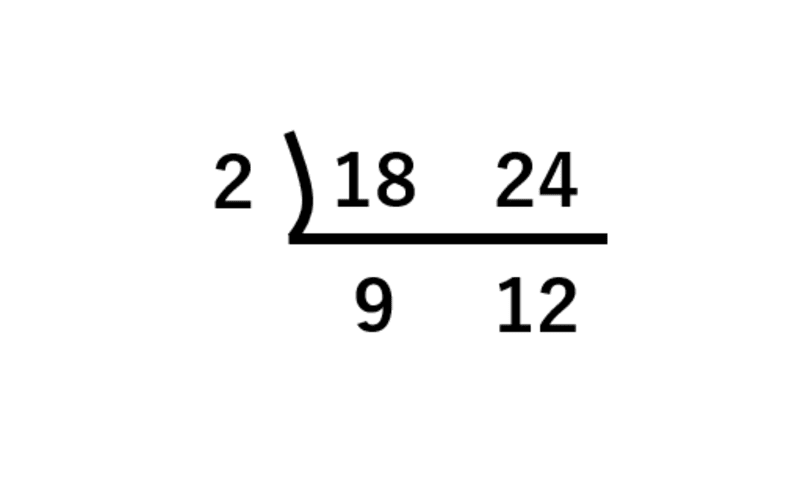
続いて9と12を割るのにふさわしいのは3なので、3を左に3と4を下段に書けば、2つの数字は互いに素です。
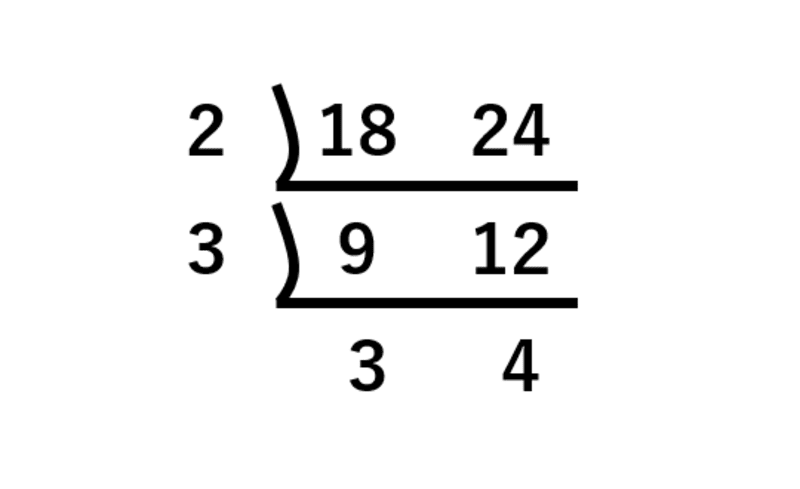
2数が互いに素となったら、割った数を全て掛け合わせた答えが最大公約数となります。よって18と24の最大公約数は2×3=6です。
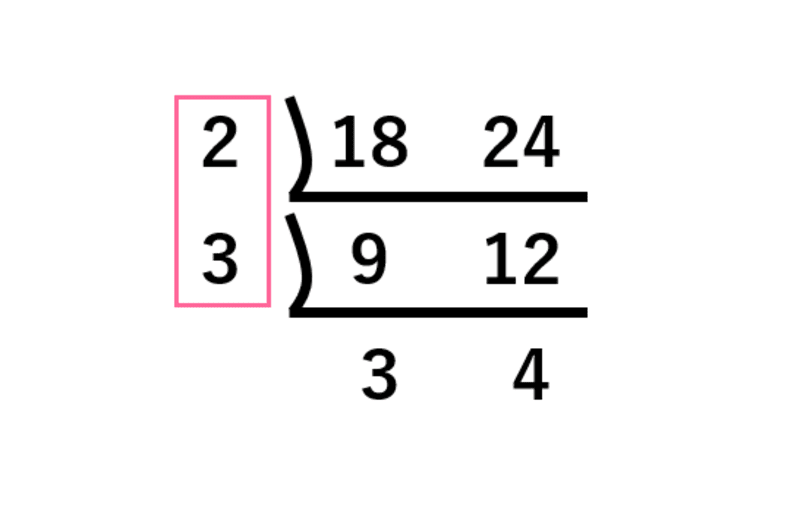
また互いに素となった2数も合わせて掛ければ、最小公倍数を求めることができます。そのため、18と24の最小公倍数は2×3×3×4=72です。
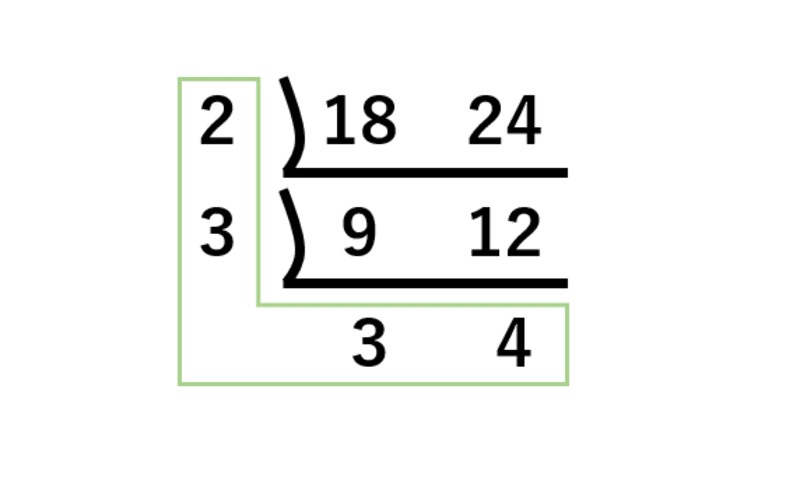
ちなみに図のようにはしごを降りるように計算していくことから、連除法ははしご算と呼ばれることもあります。
3つ以上の数における最大公約数の求め方
連除法を使えば、3つ以上の数に関する最大公約数や最小公倍数も求めることができます。ただし、最小公倍数を出す時は一工程増えるので注意しましょう。
最大公約数に関しては上記と同じように左の素数を掛け合わせるだけです。
3つ以上の数における最小公倍数の求め方
3つ以上の数に関して連除法を使う時も最大公約数に関しては、全く同じ方法で求めることができます。しかし、最小公倍数に関しては若干ややこしいです。
例えば、3つの数に関して連除法を使った時、一番最後の段が2、11、4になったとします。これら全てを割り切ることのできる数は存在しないので、最大公約数を求める連除法はこれで完了です。
しかし、2と4は互いに素ではないため、最大公約数に2、11、4を掛けても最小公倍数にはなりません。よってこの場合は11は無視してもう一度2で割り、「1、11、2」という互いに素の状態を作ってください。
全ての組み合わせが互いに素となって初めて、左列と最下段の積で最小公倍数を求めることができます。そのため、この場合の最小公倍数は「最大公約数×2×1×11×2」です。
小学生向け公約数の問題5選

問題
以下の数の組において、それぞれの数の最大公約数を求めなさい。
- 15、35
- 52、64
- 26、39
- 15、45、102
- 3、17、23
回答・解説
- 5
- 4
- 13
- 3
- 1
特に4番と5番の問題はやや難易度が高いです。
4番では一番小さな数が15と、全体的に大きな数字を扱っているものの、3つの数の公約数を探すと1と3の2つしかないことに気がつきます。
このように、登場する数が大きいからといって最大公約数も大きいとは限らない点に注意が必要です。
5番では3と17と23の公約数は1しか存在しないことに気づきます。そもそも3は1と3でしか割れないので、17も23も3で割れないことに気づけば、最大公約数は1であることはすぐに求められます。
なお、中学生〜高校生以上の方の場合、5番に登場する数字が全て素数であることに気づけば、最大公約数は1だと一瞬で導くことができます。
大学入試センター試験でも頻出?

最大公約数は共通テスト(旧センター試験)の整数問題にもよく登場します。
ユークリッドの互除法
高校数学の整数問題で扱われる数字は大きいので、最大公約数を求めるのにはユークリッドの互除法を用います。ユークリッドの互除法とは、以下のような方法のことです。
- 24÷18=1あまり6
- 18÷6=3
上記のように、最大公約数を求めたい2数のうち大きい方を小さい方で割り、次は小さい方を出た余りで割ります。同様の作業を余りが出なくなるまで繰り返し、最後の式の割る数が最大公約数です。
互いに素
高校数学の整数問題や最大公約数を考える上で重要になるのが「互いに素」という概念です。決して難しいことではありませんが、時々わからなくなってしまう人もいるので、もう一度確認しておきましょう。
先述した通り、互いに素とは公約数が1しかない2数の関係のことを指します。言い換えれば2数の最大公約数が1だということです。
例えば、12と5の公約数は1しかない(最大公約数が1)なので、12と5は「互いに素」であると言えます。
では以下の3パターンの組み合わせはどうでしょうか。
- 3と5
- 12と18
- 27と19
- 372と31
まず3と5の公約数は1だけなので、この関係性は互いに素です。このように素数同士の関係は互いに素になります。
一方で12と18の最大公約数は6です。よって12と18は互いに素でありません。
続いて27と19ですが、両者の最大公約数は1なのでこれは互いに素です。2数のどちらかが素数の場合、もう一方がその素数の倍数でなければ2数は互いに素となります。
よって、372は素数31の倍数であるため、372と31は互いに素ではありません。
センター対策の整数問題は過去問がお勧め
共通テスト(旧センター試験)の整数問題や公約数が登場する問題のパターンは限定的です。
よって基本的な考え方や解き方を覚えたら、後は過去問演習を繰り返して出題のパターンに慣れるというのが攻略のための最短ルートになります。
ただし、志望校によっては公約数の問題や互いに素を用いる証明問題が頻出であるということもあるため、その場合は問題集で整数問題の特訓をするというのも良いでしょう。
公約数・公倍数の対策におすすめ教材

ここからは公約数や公倍数の勉強におすすめの教材をいくつか紹介します。
学校の宿題・授業をしっかり理解
小学校のうちは学校の教科書レベルの内容をきちんと理解しておけば十分です。それができていれば、中学生になった後も問題なく授業についていけるでしょう。
よって学校の宿題で出されるドリルなどをサボらずにきちんとやることが大切だと言えます。
実際、将来東大に入るような子供でも、中学受験をしないなら、小学校時代は学校の教材だけで勉強しているということが多いです。
そのため、宿題を中心に学校の教材で程よく勉強し、中学以降の勉強で学力を伸ばすための基礎をしっかり作るということを意識しましょう。
タブレットで学べる教材が人気
基本的には学校の教材だけで十分ですが、補助教材として通信教育を利用するのがおすすめです。中でも昨今主流になりつつあるタブレット教材が良いでしょう。
塾に通うほどではないけれど、学校の教材にプラスしてもう少し勉強させたいという場合には通信教育がおすすめです。
タブレットを使う講座では楽しく学校の予習・復習ができることが見込まれるので、学習習慣を付けさせたいという場合にも良いでしょう。
またタブレットなら動画やアニメーションを用いた解説もあるので、算数があまり得意ではないお子さんでも、視覚的なイメージによって理解が捗るはずです。
さらにタブレット教材にはゲーム的な要素も含まれているため、勉強が嫌いなお子さんにもおすすめできます。
他にも、家庭教師や個別指導なら講師や教室の雰囲気に当たり外れがありますが、タブレット通信教育なら安定して質の高い教育を受けられるという点も魅力的です。
算数も含めて、小学生におすすめの通信教育については以下の記事で解説しています。
算数の公約数・最大公約数まとめ
算数の公約数・最大公約数まとめ
- 約数はある数を掛け算で表した時に登場する自然数
- 3つの数で連除法を使う際は最小公倍数に注意
- 算数を重点的に強化したいならRISU算数
算数の公約数・最大公約数について解説しました。
そもそも公約数とは2つの数字が共有する約数(ある数を掛け算で表した時に登場する自然数)のことです。
最も大きい公約数である最大公約数は、連除法を用いて左側の素数を全て掛け合わせることによって簡単に求められます。
なお、小学生のうちの算数学習は、基本的には学校の宿題をやることで教科書レベルのことをきちんと押さえられていれば十分です。
ただし、学校の教材+αが欲しいのであれば通信教育がおすすめです。
以上を参考に、お子さんの算数学習について考えてみてください。







